
【題目】已知函數(shù)![]() 是定義域為
是定義域為![]() 的奇函數(shù),且當
的奇函數(shù),且當![]() 時,
時,![]() ,其中
,其中![]() 是常數(shù).
是常數(shù).
(1)求![]() 的解析式;
的解析式;
(2)求實數(shù)![]() 的值,使得函數(shù)
的值,使得函數(shù)![]() ,
,![]() 的最小值為
的最小值為![]() ;
;
(3)已知函數(shù)![]() 滿足:對任何不小于
滿足:對任何不小于![]() 的實數(shù)
的實數(shù)![]() ,都有
,都有![]() ,其中
,其中![]() 為不小于
為不小于![]() 的正整數(shù)常數(shù),求證:
的正整數(shù)常數(shù),求證:![]() .
.
【答案】(1)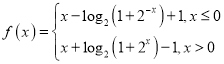 ;(2)
;(2)![]() ;(3)證明見解析.
;(3)證明見解析.
【解析】
(1)由函數(shù)![]() 是
是![]() 上的奇函數(shù)得出
上的奇函數(shù)得出![]() ,可解出
,可解出![]() ,再令
,再令![]() ,求出
,求出![]() ,利用奇函數(shù)的定義得出
,利用奇函數(shù)的定義得出![]() 的表達式,從而得出函數(shù)
的表達式,從而得出函數(shù)![]() 在
在![]() 上的解析式;
上的解析式;
(2)由題意得出![]() ,令
,令![]() ,可得出
,可得出![]() ,再分
,再分![]() 、
、![]() 、
、![]() 三種情況討論,分析該二次函數(shù)在區(qū)間
三種情況討論,分析該二次函數(shù)在區(qū)間![]() 上的單調性,得出該二次函數(shù)的最小值為
上的單調性,得出該二次函數(shù)的最小值為![]() ,求出
,求出![]() 的值;
的值;
(3)先求出![]() ,任取
,任取![]() 且
且![]() ,利用作差法證明出
,利用作差法證明出![]() ,由此得出
,由此得出![]() ,
,![]() ,
,![]() ,
,![]() ,再利用同向不等式的可加性可得出所證不等式成立.
,再利用同向不等式的可加性可得出所證不等式成立.
(1)由于函數(shù)![]() 是
是![]() 上的奇函數(shù),則
上的奇函數(shù),則![]() ,
,
那么,當![]() 時,
時,![]() .
.
當![]() 時,
時,![]() ,
,![]() ,
,
![]() .
.![]() 也適合
也適合![]() .
.
因此,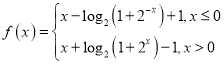 ;
;
(2)當![]() 時,
時,![]() ,
,
則![]() ,
,
令![]() ,則
,則![]() ,
,
該二次函數(shù)圖象開口向上,對稱軸為直線![]() .
.
①當![]() 時,即當
時,即當![]() 時,函數(shù)
時,函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上單調遞增,此時,
上單調遞增,此時,![]() ,解得
,解得![]() ,合乎題意;
,合乎題意;
②當![]() 時,即當
時,即當![]() 時,函數(shù)
時,函數(shù)![]() 在
在![]() 上取得最小值,即
上取得最小值,即![]() ,整理得
,整理得![]() ,解得
,解得![]() ,
,
均不符合題意;
③當![]() 時,即當
時,即當![]() 時,函數(shù)
時,函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上單調遞減,
上單調遞減,
此時,![]() ,不合乎題意.
,不合乎題意.
綜上所述,當![]() 時,函數(shù)
時,函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上的最小值為
上的最小值為![]() ;
;
(3)當![]() 時,
時,![]() .
.
當![]() 時,
時,![]() ,則
,則![]() ,
,
整理得![]() ,解得
,解得![]() .
.
任取![]() 且
且![]() ,
,
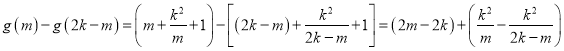
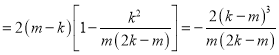 ,
,
![]() 且
且![]() ,
,![]() ,
,![]() ,所以,
,所以,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
上述不等式全部相加得![]() .
.


科目:高中數(shù)學 來源: 題型:
【題目】將三棱錐![]() 與
與![]() 拼接得到如圖所示的多面體,其中
拼接得到如圖所示的多面體,其中![]() ,
,![]() ,
,![]() ,
,![]() 分別為
分別為![]() ,
,![]() ,
,![]() ,
,![]() 的中點,
的中點,![]() .
.
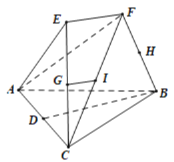
(1)當點![]() 在直線
在直線![]() 上時,證明:
上時,證明:![]() 平面
平面![]() ;
;
(2)若![]() 與
與![]() 均為面積為
均為面積為![]() 的等邊三角形,求該多面體體積的最大值.
的等邊三角形,求該多面體體積的最大值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,己知拋物線![]() ,直線
,直線![]() 交拋物線于
交拋物線于![]() 兩點,
兩點,![]() 是拋物線外一點,連接
是拋物線外一點,連接![]() 分別交地物線于點
分別交地物線于點![]() ,且
,且![]() .
.

(1)若![]() ,求點
,求點![]() 的軌跡方程.
的軌跡方程.
(2)若![]() ,且
,且![]() 平行x軸,求
平行x軸,求![]() 面積.
面積.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某中學為研究學生的身體素質與體育鍛煉時間的關系,對該校300名高三學生平均每天體育鍛煉時間進行調查,如表:(平均每天鍛煉的時間單位:分鐘).
平均每天鍛煉的時間/分鐘 |
|
|
|
|
|
|
總人數(shù) | 34 | 51 | 59 | 66 | 65 | 25 |
將學生日均體育鍛煉時間在![]() 的學生評價為“鍛煉達標”.
的學生評價為“鍛煉達標”.
(1)請根據(jù)上述表格中的統(tǒng)計數(shù)據(jù)填寫下面的![]() 列聯(lián)表;
列聯(lián)表;
鍛煉不達標 | 鍛煉達標 | 合計 | |
男 | |||
女 | 40 | 160 | |
合計 |
(2)通過計算判斷,是否能在犯錯誤的概率不超過0.05的前提下認為“鍛煉達標”與性別有關?
參考公式:![]() ,其中
,其中![]() .
.
臨界值表
| 0.10 | 0.05 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)f(x)的圖象與函數(shù)h(x)=x+![]() +2的圖象關于點A(0,1)對稱.
+2的圖象關于點A(0,1)對稱.
(1)求函數(shù)f(x)的解析式;
(2)若g(x)=f(x)+![]() ,g(x)在區(qū)間(0,2]上的值不小于6,求實數(shù)a的取值范圍.
,g(x)在區(qū)間(0,2]上的值不小于6,求實數(shù)a的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知焦點在![]() 軸上的拋物線
軸上的拋物線![]() 過點
過點![]() ,橢圓
,橢圓![]() 的兩個焦點分別為
的兩個焦點分別為![]() ,
,![]() ,其中
,其中![]() 與
與![]() 的焦點重合,過點
的焦點重合,過點![]() 與
與![]() 的長軸垂直的直線交
的長軸垂直的直線交![]() 于
于![]() ,
,![]() 兩點,且
兩點,且![]() ,曲線
,曲線![]() 是以坐標原點
是以坐標原點![]() 為圓心,以
為圓心,以![]() 為半徑的圓.
為半徑的圓.
(1)求![]() 與
與![]() 的標準方程;
的標準方程;
(2)若動直線![]() 與
與![]() 相切,且與
相切,且與![]() 交于
交于![]() ,
,![]() 兩點,求
兩點,求![]() 的面積
的面積![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知橢圓![]() 的左右焦點分別為
的左右焦點分別為![]() ,離心率為
,離心率為![]() ,
,![]() 是橢圓
是橢圓![]() 上的一個動點,且
上的一個動點,且![]() 面積的最大值為
面積的最大值為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)設直線![]() 斜率為
斜率為![]() ,且
,且![]() 與橢圓
與橢圓![]() 的另一個交點為
的另一個交點為![]() ,是否存在點
,是否存在點![]() ,使得
,使得![]() 若存在,求
若存在,求![]() 的取值范圍;若不存在,請說明理由.
的取值范圍;若不存在,請說明理由.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com