
【題目】如圖,在三棱錐 ![]() 中,
中, ![]() 底面
底面 ![]() 分別是
分別是 ![]() 的中點,
的中點, ![]() 在
在 ![]() ,且
,且 ![]() .
.
(1)求證: ![]() 平面
平面 ![]() ;
;
(2)在線段 ![]() 上是否存在點
上是否存在點 ![]() ,使二面角
,使二面角 ![]() 的大小為
的大小為 ![]() ?若存在,求出
?若存在,求出 ![]() 的長;
的長;
若不存在,請說明理由.
【答案】
(1)證明:由 ![]() ,
,![]() 是
是 ![]() 的中點,得
的中點,得 ![]() ,
,
因為 ![]() 底面
底面 ![]() ,所以
,所以 ![]() ,
,
在 ![]() 中,
中, ![]() ,所以
,所以 ![]() ,
,
因此 ![]() ,又因為
,又因為 ![]() ,
,
所以 ![]() ,
,
則 ![]() ,即
,即 ![]() ,因為
,因為 ![]() 底面
底面 ![]() ,
,
所以 ![]() ,又
,又 ![]() ,
,
又 ![]() ,所以
,所以 ![]() 平面
平面 ![]() .
.
(2)解:假設滿足條件的點 ![]() ,存在,
,存在,
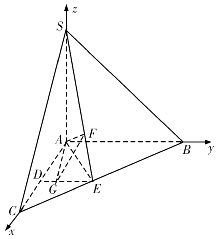
并設 ![]() ,以
,以 ![]() 為坐標原點,分別以
為坐標原點,分別以 ![]() 為
為 ![]() 軸建立空間之間坐標系
軸建立空間之間坐標系 ![]() ,
,
則 ![]() ,
,
由 ![]() ,所以
,所以 ![]() ,所以
,所以 ![]() ,
,
設平面 ![]() 的法向量為
的法向量為 ![]() ,
,
則  ,取
,取 ![]() ,得
,得 ![]() ,
,
即 ![]() ,設平面
,設平面 ![]() 的法向量為
的法向量為 ![]() ,
,
則 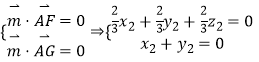 ,取
,取 ![]() ,得
,得 ![]() ,
,
即 ![]() ,
,
由二面角 ![]() 的大小為
的大小為 ![]() ,得
,得 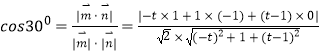 ,
,
化簡得 ![]() ,又
,又 ![]() ,求得
,求得 ![]() ,于是滿足條件的點
,于是滿足條件的點 ![]() 存在,且
存在,且 ![]() .
.
【解析】(1)根據(jù)題意由線面垂直的性質(zhì)定理即可得到線線垂直,再由已知的線線垂直結(jié)合線面垂直的判定定理即可得證。(2)根據(jù)題意結(jié)合已知條件根據(jù)題意建立空間直角坐標系,求出各個點的坐標進而求出各個向量的坐標,設出平面AFG和平面AEF的法向量,由向量垂直的坐標運算公式可求出法向量,再利用向量的數(shù)量積運算公式求出余弦值進而得到t的值于是滿足條件的點 G 存在。


 新課標快樂提優(yōu)暑假作業(yè)陜西旅游出版社系列答案
新課標快樂提優(yōu)暑假作業(yè)陜西旅游出版社系列答案 暑假銜接培優(yōu)教材浙江工商大學出版社系列答案
暑假銜接培優(yōu)教材浙江工商大學出版社系列答案科目:高中數(shù)學 來源: 題型:
【題目】北京101中學校園內(nèi)有一個“少年湖”,湖的兩側(cè)有一個音樂教室和一個圖書館,如圖,若設音樂教室在A處,圖書館在B處,為測量A,B兩地之間的距離,某同學選定了與A,B不共線的C處,構(gòu)成△ABC,以下是測量的數(shù)據(jù)的不同方案:①測量∠A,AC,BC;②測量∠A,∠B,BC;③測量∠C,AC,BC;④測量∠A,∠C,∠B. 其中一定能唯一確定A,B兩地之間的距離的所有方案的序號是_______.

查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知平面內(nèi)一動點 ![]() 到點
到點 ![]() 的距離與點
的距離與點 ![]() 到 x
到 x![]() 軸的距離的差等于1.
軸的距離的差等于1.
(1)求動點 ![]() 的軌跡
的軌跡 ![]() 的方程;
的方程;
(2)過點 ![]() 作兩條斜率存在且互相垂直的直線
作兩條斜率存在且互相垂直的直線 ![]() ,設
,設 ![]() 與軌跡
與軌跡 ![]() 相交于點
相交于點 ![]() ,
, ![]() 與軌跡
與軌跡 ![]() 相交于點
相交于點 ![]() ,求
,求 ![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知命題 ![]() ,命題方程
,命題方程 ![]() 表示焦點在
表示焦點在 ![]() 軸上的雙曲線.
軸上的雙曲線.
(1)命題 ![]() 為真命題,求實數(shù)
為真命題,求實數(shù) ![]() 的取值范圍;
的取值范圍;
(2)若命題“ ![]() ”為真,命題“
”為真,命題“ ![]() ”為假,求實數(shù)
”為假,求實數(shù) ![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】函數(shù) ![]() .
.
(1)求函數(shù) ![]() 的最大值;
的最大值;
(2)對于任意 ![]() ,且
,且 ![]() ,是否存在實數(shù)
,是否存在實數(shù) ![]() ,使
,使 ![]() 恒成立,若存在求出
恒成立,若存在求出 ![]() 的范圍,若不存在,說明理由;
的范圍,若不存在,說明理由;
(3)若正項數(shù)列 ![]() 滿足
滿足 ![]() ,且數(shù)列
,且數(shù)列 ![]() 的前
的前 ![]() 項和為
項和為 ![]() ,試判斷
,試判斷 ![]() 與
與 ![]() 的大小,并加以證明.
的大小,并加以證明.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】給出下列四個命題:①若![]() ,則
,則![]() ;②若
;②若![]() ,則
,則![]() ;③若
;③若![]() ,則
,則![]() ;④若
;④若![]() ,
, ![]() 且
且![]() ,則
,則![]() 的最小值為9;其中正確命題的序號是______(將你認為正確的命題序號都填上).
的最小值為9;其中正確命題的序號是______(將你認為正確的命題序號都填上).
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】下列命題錯誤的是( )
A.命題“若 ![]() ,則
,則 ![]() ”的逆命題為“若
”的逆命題為“若 ![]() ,則
,則 ![]() ”
”
B.對于命題 ![]() ,使得
,使得 ![]() ,則
,則 ![]() ,則
,則 ![]()
C.“ ![]() ”是“
”是“ ![]() ”的充分不必要條件
”的充分不必要條件
D.若 ![]() 為假命題,則
為假命題,則 ![]() 均為假命題
均為假命題
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知等差數(shù)列{an}的公差d≠0,它的前n項和為Sn,若S5=70,且a2,a7,a22成等比數(shù)列.
(1)求數(shù)列{an}的通項公式;
(2)設數(shù)列![]() 的前n項和為Tn,求證:
的前n項和為Tn,求證: ![]() ≤Tn<
≤Tn<![]() .
.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com