
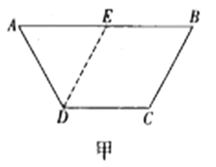
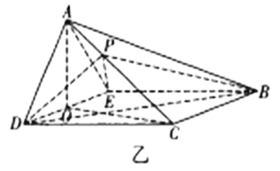
【題目】如圖甲,在等腰梯形![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 的中點.將
的中點.將![]() 沿
沿![]() 折起,使二面角
折起,使二面角![]() 為
為![]() ,連接
,連接![]() ,
,![]() 得到四棱錐
得到四棱錐![]() (如圖乙),
(如圖乙),![]() 為
為![]() 的中點,
的中點,![]() 是棱
是棱![]() 上一點.
上一點.
(1)求證:當![]() 為
為![]() 的中點時,平面
的中點時,平面![]() 平面
平面![]() ;
;
(2)是否存在一點![]() ,使平面
,使平面![]() 與平面
與平面![]() 所成的銳二面角為
所成的銳二面角為![]() ,若存在,求
,若存在,求![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
【答案】(1)證明見解析(2)存在;![]()
【解析】
(1)由題易證得![]() ,根據等腰三角形的性質可得
,根據等腰三角形的性質可得![]() ,
,![]() ,則
,則![]() 平面
平面![]() ,由平行線的性質可知
,由平行線的性質可知![]() 平面
平面![]() ,則
,則![]() ,再利用
,再利用![]() 可得
可得![]() ,即可求證;
,即可求證;
(2)由題以![]() 為原點,
為原點,![]() 為坐標軸建立空間坐標系
為坐標軸建立空間坐標系![]() ,設
,設![]() ,
,![]() ,分別求得平面
,分別求得平面![]() 與平面
與平面![]() 的法向量,進而利用數量積求解即可.
的法向量,進而利用數量積求解即可.
(1)證明:連接![]() ,
,![]() ,
,

由題,因為![]() ,
,![]() 為
為![]() 的中點,所以
的中點,所以![]() ,
,
因為![]() 是
是![]() 的中點,所以
的中點,所以![]() ,
,
又![]() ,所以四邊形
,所以四邊形![]() 是平行四邊形,所以
是平行四邊形,所以![]() ,即
,即![]() ,
,
所以![]() ,且
,且![]() ,
,
又![]() ,所以
,所以![]() 平面
平面![]() ,
,
因為![]() ,所以
,所以![]() 平面
平面![]() ,
,
因為![]() 平面
平面![]() ,所以
,所以![]() ,
,
又因為![]() ,
,![]() 為
為![]() 的中點,所以
的中點,所以![]() ,
,
又![]() ,所以
,所以![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
(2)解:存在,
以![]() 為原點,
為原點,![]() 為坐標軸建立如圖所示的坐標系
為坐標軸建立如圖所示的坐標系![]() ,如圖所示,
,如圖所示,
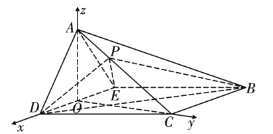
不妨設棱長![]() ,由(1)可知
,由(1)可知![]() 是等邊三角形,
是等邊三角形,
則![]() ,
,![]() ,
,![]() ,
,![]() ,
,
設![]() ,且
,且![]() ,
,![]() ,
,
則![]() ,
,
可得![]() ,則
,則![]() ,
,![]() ,
,
設![]() 是平面
是平面![]() 的一個法向量,
的一個法向量,
則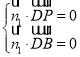 ,即
,即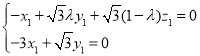 ,
,
令![]() ,則
,則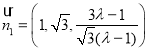 ,
,
由(1)知![]() 平面
平面![]() ,則
,則![]() 是平面
是平面![]() 的一個法向量,
的一個法向量,
若存在點![]() ,使平面
,使平面![]() 與平面
與平面![]() 所成的銳二面角為
所成的銳二面角為![]() ,
,
則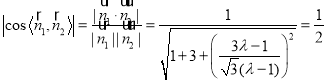 ,
,
解得![]() ,
,
所以存在點![]() ,使平面
,使平面![]() 與平面
與平面![]() 所成的銳二面角為
所成的銳二面角為![]() ,此時
,此時![]() .
.


科目:高中數學 來源: 題型:
【題目】已知數組![]() ,如果數組
,如果數組![]() 滿足
滿足![]() ,且
,且![]() ,其中
,其中![]()
![]() ,則稱
,則稱![]() 為
為![]() 的“兄弟數組”.
的“兄弟數組”.
(1)寫出數組![]() 的“兄弟數組”
的“兄弟數組”![]() ;
;
(2)若![]() 的“兄弟數組”是
的“兄弟數組”是![]() ,試證明:
,試證明:![]() 成等差數列;
成等差數列;
(3)若![]() 為偶數,且
為偶數,且![]() 的“兄弟數組”是
的“兄弟數組”是![]() ,求證:
,求證:![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=lnx﹣ax+1(a∈R).
(1)求f(x)的單調區間;
(2)設g(x)=lnx![]() ,若對任意的x1∈(0,+∞),存在x2∈(1,+∞),使得f(x1)<g(x2)成立,求實數a的取值范圍.
,若對任意的x1∈(0,+∞),存在x2∈(1,+∞),使得f(x1)<g(x2)成立,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校為了解高三年級不同性別的學生對體育課改上自習課的態度(肯定還是否定),進行了如下的調查研究.全年級共有![]() 名學生,男女生人數之比為
名學生,男女生人數之比為![]() ,現按分層抽樣方法抽取若干名學生,每人被抽到的概率均為
,現按分層抽樣方法抽取若干名學生,每人被抽到的概率均為![]() .
.
(1)求抽取的男學生人數和女學生人數;
(2)通過對被抽取的學生的問卷調查,得到如下![]() 列聯表:
列聯表:
否定 | 肯定 | 總計 | |
男生 | 10 | ||
女生 | 30 | ||
總計 |
①完成列聯表;
②能否有![]() 的把握認為態度與性別有關?
的把握認為態度與性別有關?
(3)若一班有![]() 名男生被抽到,其中
名男生被抽到,其中![]() 人持否定態度,
人持否定態度,![]() 人持肯定態度;二班有
人持肯定態度;二班有![]() 名女生被抽到,其中
名女生被抽到,其中![]() 人持否定態度,
人持否定態度,![]() 人持肯定態度.
人持肯定態度.
現從這![]() 人中隨機抽取一男一女進一步詢問所持態度的原因,求其中恰有一人持肯定態度一人持否定態度的概率.
人中隨機抽取一男一女進一步詢問所持態度的原因,求其中恰有一人持肯定態度一人持否定態度的概率.
解答時可參考下面臨界值表:
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】三國時代吳國數學家趙爽所注《周髀算經》中給出了勾股定理的絕妙證明.下面是趙爽的弦圖及注文,弦圖是一個以勾股形之弦為邊的正方形,其面積稱為弦實.圖中包含四個全等的勾股形及一個小正方形,分別涂成紅(朱)色及黃色,其面積稱為朱實、黃實,利用![]() ,化簡,得
,化簡,得![]() .設勾股形中勾股比為
.設勾股形中勾股比為![]() ,若向弦圖內隨機拋擲
,若向弦圖內隨機拋擲![]() 顆圖釘(大小忽略不計),則落在黃色圖形內的圖釘數大約為( )
顆圖釘(大小忽略不計),則落在黃色圖形內的圖釘數大約為( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,直線l的參數方程為![]() (
(![]() 為參數),在以O為極點,x軸的非負半軸為極軸的極坐標系中,曲線C的極坐標方程為
為參數),在以O為極點,x軸的非負半軸為極軸的極坐標系中,曲線C的極坐標方程為![]()
(1)求曲線C的直角坐標方程
(2)設直線l與x軸交于點P,且與曲線C相交與A、B兩點,若![]() 是
是![]() 與
與![]() 的等比中項,求實數m的值
的等比中項,求實數m的值
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖為服用同等劑量的三種新藥后血藥濃度![]() 的變化情況,其中點
的變化情況,其中點![]() 的橫坐標表示服用第
的橫坐標表示服用第![]() 種藥后血藥濃度達峰(最高濃度)時間,其它點的橫坐標分別表示服用三種新藥后血藥濃度首次降到峰值一半時所用的時間(單位:
種藥后血藥濃度達峰(最高濃度)時間,其它點的橫坐標分別表示服用三種新藥后血藥濃度首次降到峰值一半時所用的時間(單位:![]() ),點
),點![]() 的縱坐標表示第
的縱坐標表示第![]() 種藥的血藥濃度的峰值
種藥的血藥濃度的峰值![]() . 記
. 記![]() 為服用第
為服用第![]() 種藥后達到血藥濃度峰值時,血藥濃度提高的平均速度,記
種藥后達到血藥濃度峰值時,血藥濃度提高的平均速度,記![]() 為服用第
為服用第![]() 種藥后血藥濃度從峰值首次降到峰值的一半所用的時間,則
種藥后血藥濃度從峰值首次降到峰值的一半所用的時間,則![]() 中最小的,
中最小的,![]() 中最大的分別是( )
中最大的分別是( )
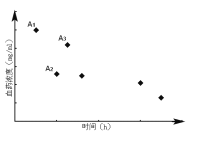
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系中,曲線![]() 的參數方程為
的參數方程為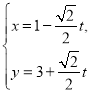 (
(![]() 為參數).以坐標原點為極點,
為參數).以坐標原點為極點,![]() 軸正半軸為極軸,建立極坐標系,曲線
軸正半軸為極軸,建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)寫出![]() 的普通方程及
的普通方程及![]() 的直角坐標方程;
的直角坐標方程;
(2)設點![]() 在
在![]() 上,點
上,點![]() 在
在![]() 上,求
上,求![]() 的最小值及此時點
的最小值及此時點![]() 的直角坐標.
的直角坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com