
【題目】長時間用手機上網嚴重影響著學生的身體健康,某校為了解![]() 兩班學生手機上網的時長,分別從這兩個班中隨機抽取5名同學進行調查,將他們平均每周手機上網的時長作為樣本,繪制成莖葉圖如圖所示(圖中莖葉表示十位數字,葉表示個位數字).
兩班學生手機上網的時長,分別從這兩個班中隨機抽取5名同學進行調查,將他們平均每周手機上網的時長作為樣本,繪制成莖葉圖如圖所示(圖中莖葉表示十位數字,葉表示個位數字).
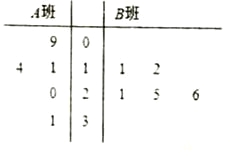
(1)分別求出圖中所給兩組樣本數據的平均值,并據此估計,哪個班的學生平均上網時間較長;
(2)從![]() 班的樣本數據中隨機抽取一個不超過19的數據記為
班的樣本數據中隨機抽取一個不超過19的數據記為![]() ,從
,從![]() 班的樣本數據中隨機抽取一個不超過21的數據記為
班的樣本數據中隨機抽取一個不超過21的數據記為![]() ,求
,求![]() 的概率.
的概率.
【答案】(1)![]() 班學生每周平均上網時間較長(2)
班學生每周平均上網時間較長(2)![]() 的概率
的概率![]()
【解析】試題分析:(1)由莖葉圖出![]() 班,
班,![]() 班的樣本數據,分別求出兩組樣本數據的平均值,樣本數據的平均值較大的平均上網時間較長;(2)分別讀出
班的樣本數據,分別求出兩組樣本數據的平均值,樣本數據的平均值較大的平均上網時間較長;(2)分別讀出![]() 班的樣本數據中不超過19的數據
班的樣本數據中不超過19的數據![]() 的有3個,
的有3個,![]() 班的樣本數據中不超過21的數據
班的樣本數據中不超過21的數據![]() 也有3個,則用列舉法列出從
也有3個,則用列舉法列出從![]() 班和
班和![]() 班的樣本數據中各隨機抽取一個的情況共9種,由其中
班的樣本數據中各隨機抽取一個的情況共9種,由其中![]() 的情況有兩種,根據古典概型可求
的情況有兩種,根據古典概型可求![]() 的概率
的概率
試題解析:(1)![]() 班樣本數據的平均值為
班樣本數據的平均值為![]()
由此估計![]() 班學生每周平均上網時間17小時;
班學生每周平均上網時間17小時;
![]() 班樣本數據的平均值為
班樣本數據的平均值為![]()
由此估計![]() 班學生每周平均上網時間較長.
班學生每周平均上網時間較長.
(2)![]() 班的樣本數據中不超過19的數據
班的樣本數據中不超過19的數據![]() 的有3個,分別為:9,11,14,
的有3個,分別為:9,11,14,
![]() 班的樣本數據中不超過21的數據
班的樣本數據中不超過21的數據![]() 也有3個,分別為:11,12,21,
也有3個,分別為:11,12,21,
從![]() 班和
班和![]() 班的樣本數據中各隨機抽取一個共有:9種不同情況,
班的樣本數據中各隨機抽取一個共有:9種不同情況,
分別為:![]()
其中![]() 的情況有
的情況有![]() 兩種,故
兩種,故![]() 的概率
的概率![]() .
.


 周周清檢測系列答案
周周清檢測系列答案 輕巧奪冠周測月考直通高考系列答案
輕巧奪冠周測月考直通高考系列答案科目:高中數學 來源: 題型:
【題目】某校高一年級某次數學競賽隨機抽取![]() 名學生的成績,分組為
名學生的成績,分組為![]() ,統計后得到頻率分布直方圖如圖所示:
,統計后得到頻率分布直方圖如圖所示:
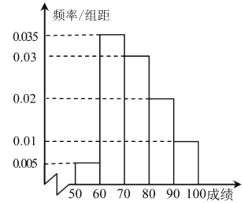
(1)試估計這組樣本數據的眾數和中位數(結果精確到![]() );
);
(2)年級決定在成績![]() 中用分層抽樣抽取
中用分層抽樣抽取![]() 人組成一個調研小組,對髙一年級學生課外學習數學的情況做一個調查,則在
人組成一個調研小組,對髙一年級學生課外學習數學的情況做一個調查,則在![]() 這三組分別抽取了多少人?
這三組分別抽取了多少人?
(3)現在要從(2)中抽取的![]() 人中選出正副
人中選出正副![]() 個小組長,求成績在
個小組長,求成績在![]() 中至少有
中至少有![]() 人當選為正、副小組長的概率.
人當選為正、副小組長的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某商場舉行有獎促銷活動,顧客購買一定金額商品后即可抽獎,每次抽獎都從裝有4個紅球、6個白球的甲箱和裝有5個紅球、5個白球的乙箱中,各隨機摸出1個球,在摸出的2個球中,若都是紅球,則獲一等獎;若只有1個紅球,則獲二等獎;若沒有紅球,則不獲獎.
(1)求顧客抽獎1次能獲獎的概率;
(2)若某顧客有3次抽獎機會,記該顧客在3次抽獎中獲一等獎的次數為![]() ,求
,求![]() 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“開門大吉”是某電視臺推出的游戲益智節目.選手面對![]() 號
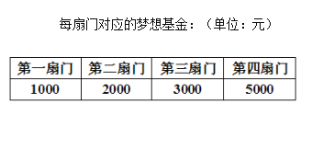
號![]() 扇大門,依次按響門上的門鈴,門鈴會播放一段音樂(將一首經典流行歌曲以單音色旋律的方式演繹),選手需正確回答出這首歌的名字,方可獲得該扇門對應的家庭夢想基金.正確回答每一扇門后,選手可自由選擇帶著獎金離開比賽,還可繼續挑戰后面的門以獲得更多獎金.(獎金金額累加)但是一旦回答錯誤,獎金將清零,選手也會離開比賽.在一次場外調查中,發現參加比賽的選手多數分為兩個年齡段:
扇大門,依次按響門上的門鈴,門鈴會播放一段音樂(將一首經典流行歌曲以單音色旋律的方式演繹),選手需正確回答出這首歌的名字,方可獲得該扇門對應的家庭夢想基金.正確回答每一扇門后,選手可自由選擇帶著獎金離開比賽,還可繼續挑戰后面的門以獲得更多獎金.(獎金金額累加)但是一旦回答錯誤,獎金將清零,選手也會離開比賽.在一次場外調查中,發現參加比賽的選手多數分為兩個年齡段:![]() ;
;![]() (單位:歲),其猜對歌曲名稱與否人數如圖所示.
(單位:歲),其猜對歌曲名稱與否人數如圖所示.
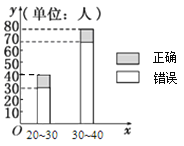
(1)寫出![]() 列聯表:判斷是否有
列聯表:判斷是否有![]() 的把握認為猜對歌曲名稱與否與年齡有關?
的把握認為猜對歌曲名稱與否與年齡有關?
說明你的理由.(下面的臨界值表供參考)

(2)若某選手能正確回答第一、二、三、四扇門的概率分別為![]() ,
,![]() ,
,![]() ,
,![]() ,正確回答一個問題后,選擇繼續回答下一個問題的概率是
,正確回答一個問題后,選擇繼續回答下一個問題的概率是![]() ,且各個問題回答正確與否互不影響.設該選手所獲夢想基金總數為
,且各個問題回答正確與否互不影響.設該選手所獲夢想基金總數為![]() ,求
,求![]() 的分布列及數學期望.
的分布列及數學期望.
(參考公式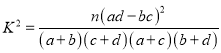 其中
其中![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一個袋中裝有四個形狀大小完全相同的球,球的編號分別為1,2,3,4.
(1)從袋中隨機取出兩個球,求取出的球的編號之和不大于4的概率.
(2)先從袋中隨機取一個球,該球的編號為m,將球放回袋中,然后再從袋中隨機取一個球,該球的編號為n,求n<m+2的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
: ![]() (
(![]() )的兩個焦點為
)的兩個焦點為![]() ,
, ![]() ,離心率為
,離心率為![]() ,點
,點![]() ,
, ![]() 在橢圓上,
在橢圓上, ![]() 在線段
在線段![]() 上,且
上,且![]() 的周長等于
的周長等于![]() .
.
(Ⅰ)求橢圓![]() 的標準方程;
的標準方程;
(Ⅱ)過圓![]() :
: ![]() 上任意一點
上任意一點![]() 作橢圓
作橢圓![]() 的兩條切線
的兩條切線![]() 和
和![]() 與圓
與圓![]() 交于點
交于點![]() ,
, ![]() ,求
,求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線![]() ,
, ![]() 是焦點,直線
是焦點,直線![]() 是經過點
是經過點![]() 的任意直線.
的任意直線.
(Ⅰ)若直線![]() 與拋物線交于
與拋物線交于![]() 、
、![]() 兩點,且
兩點,且![]() (
(![]() 是坐標原點,
是坐標原點, ![]() 是垂足),求動點
是垂足),求動點![]() 的軌跡方程;
的軌跡方程;
(Ⅱ)若![]() 、
、![]() 兩點在拋物線
兩點在拋物線![]() 上,且滿足
上,且滿足![]() ,求證:直線
,求證:直線![]() 必過定點,并求出定點的坐標.
必過定點,并求出定點的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點![]() ,橢圓
,橢圓![]()
![]() 的離心率為
的離心率為![]() ,
,![]() 是橢圓的右焦點,直線
是橢圓的右焦點,直線![]() 的斜率為
的斜率為![]() ,
,![]() 為坐標原點.
為坐標原點.
(I)求![]() 的方程;
的方程;
(II)設過點![]() 的動直線
的動直線![]() 與
與![]() 相交于
相交于![]() 兩點,當
兩點,當![]() 的面積最大時,求
的面積最大時,求![]() 的方程
的方程
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com