【題目】如圖，已知在四棱錐
中，
底面
，
，
，
，
，點
為棱
的中點,
（1）試在棱
上確定一點
，使平面
平面
，說明理由；
（2）若
為棱上一點，滿足
，求二面角
的余弦值.
科目：高中數學 來源： 題型：
【題目】某市一次全市高中男生身高統計調查數據顯示：全市
名男生的身高服從正態分布
．現從某學校高三年級男生中隨機抽取
名測量身高，測量發現被測學生身高全部介于
和
之間，將測量結果按如下方式分組： 
， 
，…， 
，得到的頻率分布直方圖如圖所示．
（Ⅰ）試評估該校高三年級男生在全市高中男生中的平均身高狀況；
（Ⅱ）求這
名男生身高在
以上（含
）的人數；
（Ⅲ）在這
名男生身高在
以上（含
）的人中任意抽取
人，該
人中身高排名（從高到低）在全市前
名的人數記力
，求
的數學期望．
參考數據：若
，則
，
， 
．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】2018年秋季，我省高一年級全面實行新高考政策，為了調查學生對新政策的了解情況，準備從某校高一
三個班級抽取10名學生參加調查.已知三個班級學生人數分別為40人，30人，30人.考慮使用簡單隨機抽樣、分層抽樣和系統抽樣三種方案，使用簡單隨機抽樣和分層抽樣時，將學生按三個班級依次統一編號為1,2，…，100；使用系統抽樣，將學生統一編號為1,2，…，100，并將整個編號依次分為10段.如果抽得的號碼有下列四種情況：
①7,17,27,37,47,57,67,77，87,97；②3,9,15,33,43,53,65,75,85,95；
③9,19,29,39,49,59,69,79,89,99,；④2,12,22,32,42,52,62,73,83,96.
關于上述樣本的下列結論中，正確的是（ ）
A. ①③都可能為分層抽樣 B. ②④都不能為分層抽樣
C. ①④都可能為系統抽樣 D. ②③都不能為系統抽樣
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某調查機構對本市小學生課業負擔情況進行了調查，設平均每人每天做作業的時間為
分鐘，有1200名小學生參加了此項調查，調查所得到的數據用程序框圖處理（如圖），若輸出的結果是840，若用樣本頻率估計概率，則平均每天做作業的時間在0～60分鐘內的學生的概率是（ ）
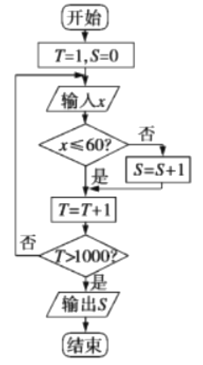
A. 0.32 B. 0.36 C. 0.7 D. 0.84
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知圓O：
，直線l：
．
若直線l與圓O交于不同的兩點A，B，當
時，求實數k的值；
若
，P是直線上的動點，過P作圓O的兩條切線PC、PD，切點分別為C、D，試探究：直線CD是否過定點
若存在，請求出定點的坐標；若不存在，請說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知命題
函數
在
上單調遞減；命題
曲線
為雙曲線．
（Ⅰ）若“
且
”為真命題，求實數
的取值范圍；
（Ⅱ）若“或”為真命題，“且”為假命題，求實數的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
(其中
為常量,且
)的圖像經過點
．
（1）求
的值；
（2）當
時,函數
的圖像恒在函數
圖像的上方,求實數
的取值范圍；
（3）是否存在實數
,使得函數
的定義域為
,值域為
?若存在,求出的值；若不存在,則說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知底面為正方形的四棱錐
，各側棱長都為
，底面面積為16，以
為球心，2為半徑作一個球，則這個球與四棱錐
相交部分的體積是（ ）
A. 
B. 
C. 
D. 
【答案】C
【解析】構造棱長為4的正方體,四棱錐O-ABCD的頂點O為正方體的中心,底面與正方體的一個底面重合.可知所求體積是正方體內切球體積的
,所以這個球與四棱錐O-ABCD相交部分的體積是: 
.
本題選擇C選項.
點睛：與球有關的組合體問題，一種是內切，一種是外接．解題時要認真分析圖形，明確切點和接點的位置，確定有關元素間的數量關系，并作出合適的截面圖，求幾何體的體積，要注意分割與補形．將不規則的幾何體通過分割或補形將其轉化為規則的幾何體求解．
【題型】單選題
【結束】
13
【題目】若
，
為第二象限角，則
__________．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
