
【題目】如圖,在四棱錐P﹣ABCD中,PD⊥平面ABCD,四邊形ABCD是菱形,AC=2,BD=2 ![]() ,E是PB上任意一點.
,E是PB上任意一點. 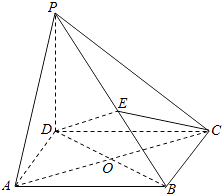
(1)求證:AC⊥DE;
(2)已知二面角A﹣PB﹣D的余弦值為 ![]() ,若E為PB的中點,求EC與平面PAB所成角的正弦值.
,若E為PB的中點,求EC與平面PAB所成角的正弦值.
【答案】
(1)證明:∵PD⊥平面ABCD,AC平面ABCD
∴PD⊥AC
又∵ABCD是菱形,∴BD⊥AC,BD∩PD=D
∴AC⊥平面PBD,∵DE平面PBD
∴AC⊥DE…(6分)
(2)解:分別以OA,OB,OE方向為x,y,z軸建立空間直角坐標系,設PD=t,則 ![]()
由(1)知:平面PBD的法向量為 ![]() ,
,
令平面PAB的法向量為 ![]() ,則根據
,則根據  得
得 ![]() ∴
∴ ![]()
因為二面角A﹣PB﹣D的余弦值為 ![]() ,則
,則 ![]() ,即
,即  ,∴
,∴ ![]()
∴ ![]()
設EC與平面PAB所成的角為θ,
∵ ![]() ,
, ![]()
∴ ![]()

【解析】(1)證明線線垂直,正弦證明線面垂直,即證AC⊥平面PBD;(2)分別以OA,OB,OE方向為x,y,z軸建立空間直角坐標系,設PD=t,用坐標表示點,求得平面PBD的法向量為 ![]() ,平面PAB的法向量為
,平面PAB的法向量為 ![]() ,根據二面角A﹣PB﹣D的余弦值為
,根據二面角A﹣PB﹣D的余弦值為 ![]() ,可求t的值,從而可得P的坐標,再利用向量的夾角公式,即可求得EC與平面PAB所成的角.
,可求t的值,從而可得P的坐標,再利用向量的夾角公式,即可求得EC與平面PAB所成的角.
【考點精析】解答此題的關鍵在于理解空間中直線與直線之間的位置關系的相關知識,掌握相交直線:同一平面內,有且只有一個公共點;平行直線:同一平面內,沒有公共點;異面直線: 不同在任何一個平面內,沒有公共點,以及對空間角的異面直線所成的角的理解,了解已知![]() 為兩異面直線,A,C與B,D分別是
為兩異面直線,A,C與B,D分別是![]() 上的任意兩點,
上的任意兩點,![]() 所成的角為
所成的角為![]() ,則
,則 .
.


科目:高中數學 來源: 題型:
【題目】已知函數 ![]() ,則f(x)是( )
,則f(x)是( )
A.周期為π,圖象關于點 ![]() 對稱的函數
對稱的函數
B.最大值為2,圖象關于點 ![]() 對稱的函數
對稱的函數
C.周期為2π,圖象關于點 ![]() 對稱的函數
對稱的函數
D.最大值為2,圖象關于直線 ![]() 對稱的函數
對稱的函數
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一只小蜜蜂在一個棱長為3的正方體玻璃容器內隨機飛行,若蜜蜂在飛行過程中與正方體玻璃容器6個表面中至少有一個的距離不大于1,則就有可能撞到玻璃上面不安全,若始終保持與正方體玻璃容器6個表面的距離均大于1,則飛行是安全的,假設蜜蜂在正方體玻璃容器內飛行到每一位置可能性相同,那么蜜蜂飛行是安全的概率是 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一個盒子中裝有4張卡片,每張卡片上寫有1個數字,數字分別是1,2,3,4,現從盒子中隨機抽取卡片.
(1)若一次從中隨機抽取3張卡片,求3張卡片上數字之和大于或等于8的概率;
(2)若隨機抽取1張卡片,放回后再隨機抽取1張卡片,求兩次抽取的卡片中至少一次抽到數字3的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某超市連鎖店統計了城市甲、乙的各16臺自動售貨機在中午12:00至13:00間的銷售金額,并用莖葉圖表示如圖.則有( ) 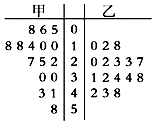
A.甲城銷售額多,乙城不夠穩定
B.甲城銷售額多,乙城穩定
C.乙城銷售額多,甲城穩定
D.乙城銷售額多,甲城不夠穩定
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“奶茶妹妹”對某時間段的奶茶銷售量及其價格進行調查,統計出售價x元和銷售量y杯之間的一組數據如下表所示:
價格x | 5 | 5.5 | 6.5 | 7 |
銷售量y | 12 | 10 | 6 | 4 |
通過分析,發現銷售量y對奶茶的價格x具有線性相關關系.
(Ⅰ)求銷售量y對奶茶的價格x的回歸直線方程;
(Ⅱ)欲使銷售量為13杯,則價格應定為多少?
注:在回歸直線y= ![]() 中,
中, 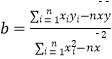 ,
, ![]() =
= ![]() ﹣
﹣ ![]() .
. ![]() =146.5.
=146.5.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=x|x﹣a|+2x(a∈R)
(1)當a=4時,解不等式f(x)≥8;
(2)當a∈[0,4]時,求f(x)在區間[3,4]上的最小值;
(3)若存在a∈[0,4],使得關于x的方程f(x)=tf(a)有3個不相等的實數根,求實數t的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設無窮等差數列{an}的前n項和為Sn , 已知a1=1,S3=12.
(1)求a24與S7的值;
(2)已知m、n均為正整數,滿足am=Sn . 試求所有n的值構成的集合.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com