【題目】已知函數
.
（1）求
的最小正周期；
（2）求在區間
上對稱軸、對稱中心及其最值.
【答案】(1)最小正周期為
(2)對稱軸
，對稱中心為
，最大值為
，最小值為
【解析】
(1)根據同角三角函數關系式的平方和關系、降冪公式、輔助角公式把函數的解析式化簡成正弦型函數解析形式,最后根據最小正周期公式求出函數的最小正周期；
(2)利用正弦型函數的對稱性和單調性,求出
在區間
上對稱軸、對稱中心及其最值
解：(1)因為
,
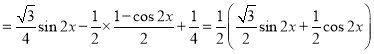
所以，函數的最小正周期為
.
(2)由(1)知
，
因為
，所以
，①
令
，得
，
所以，即為所求函數在上的對稱軸；
令
，得
，所以
，
所以函數在上的對稱中心為；（＊）
易判斷函數在
上單調遞增；在
上單調遞增.
所以，
，
，
，
故函數在區間上最大值為，最小值為.
【另解】
接（＊）式
由①得
，所以
，
故函數在區間上最大值為，最小值為.
教材全解字詞句篇系列答案科目：高中數學 來源： 題型：
【題目】我國古代數學名著《九章算術》中記載了有關特殊幾何體的定義：陽馬指底面為矩形，一側棱垂直于底面的四棱錐，塹堵指底面是直角三角形，且側棱垂直于底面的三棱柱.
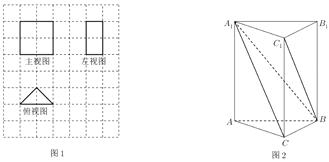
（1）某塹堵的三視圖，如圖1，網格中的每個小正方形的邊長為1，求該塹堵的體積；
（2）在塹堵
中，如圖2，
，若
，當陽馬
的體積最大時，求二面角
的大小.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】張軍自主創業，在網上經營一家干果店，銷售的干果中有松子、開心果、腰果、核桃，價格依次為120元/千克、80元/千克、70元/千克、40元千克，為增加銷量，張軍對這四種干果進行促銷:一次購買干果的總價達到150元，顧客就少付x(2x∈Z)元.每筆訂單顧客網上支付成功后，張軍會得到支付款的80%.
①若顧客一次購買松子和腰果各1千克，需要支付180元，則x=________；
②在促銷活動中，為保證張軍每筆訂單得到的金額均不低于促銷前總價的七折，則x的最大值為_____.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知數列
的前
項和為
，
且滿足:
(1)證明：是等比數列，并求數列的通項公式.
(2)設
，若數列
是等差數列，求實數
的值；
(3)在(2)的條件下，設
記數列
的前項和為
，若對任意的
存在實數
,使得
,求實數的最大值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖：已知某公園的四處景觀分別位于等腰梯形
的四個頂點處，其中
，
兩地的距離為
千米，
，
兩地的距離為
千米，
.現擬規劃在
(不包括端點)路段上增加一個景觀
，并建造觀光路直接通往處，造價為每千米
萬元，又重新裝飾
路段，造價為每千米
萬元.
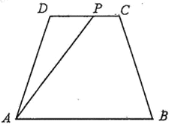
(1)若擬修建觀光路
路段長為
千米，求路段的造價；
(2)設
，當
為何值時，，段的總造價最低.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設
，
是兩條不同的直線，
，
，
是三個不同的平面，給出下列四個命題：
①若
，
，則，為異面直線； ②若
，
，
，則
；
③若
，，則
； ④若，
，
，則.
則上述命題中真命題的序號為（ ）
A.①②B.③④C.②D.②④
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知圓
： 
經過橢圓
： 
的左右焦點
，且與橢圓
在第一象限的交點為
，且
三點共線，直線
交橢圓
于
， 
兩點，且
（
）.
（1）求橢圓
的方程；
（2）當三角形
的面積取得最大值時，求直線
的方程.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某射擊小組有甲、乙、丙三名射手，已知甲擊中目標的概率是
，甲、丙二人都沒有擊中目標的概率是
，乙、丙二人都擊中目標的概率是
.甲乙丙是否擊中目標相互獨立.
（1）求乙、丙二人各自擊中目標的概率；
（2）設乙、丙二人中擊中目標的人數為X，求X的分布列和數學期望.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
