Question

（2011•重慶二模）已知實數x，y滿足

2x-y≥0 x≤1 x+y+1≥0

，則Z=︳x-y ︳的最大值是（　　）

A．1

B．2

C．3

D．4

Answer 1

分析：作出題中不等式組表示的平面區域，得如圖的△ABC及其內部，再將直線l：t=x-y對應的直線進行平移，觀察截距的變化可得-1≤t≤3，由此可得Z=|x-y|的最大值是3．

解答：解：作出不等式組

2x-y≥0 x≤1 x+y+1≥0

表示的平面區域，
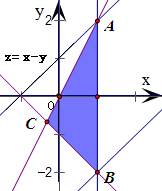
得到如圖的△ABC及其內部，
其中A（1，2），B（1，-2），C（-

1

3

，-

2

3

）
設t=F（x，y）=x-y，將直線l：t=x-y進行平移，
當l經過點A時，目標函數z達到最小值；當l經過點B時，目標函數z達到最大值
∴t_最大值=F（1，-2）=3，t_最大值=F（1，2）=-1
∴Z=|x-y|∈[0，3]，可得Z=|x-y|的最大值是3
故選：C

點評：本題給出二元一次不等式組，求目標函數Z=|x-y|︳的最大值，著重考查了二元一次不等式組表示的平面區域和簡單的線性規劃等知識，屬于基礎題．