
【題目】棉花的纖維長度是評價棉花質量的重要指標,某農科所的專家在土壤環境不同的甲、乙兩塊實驗地分別種植某品種的棉花,為了評價該品種的棉花質量,在棉花成熟后,分別從甲、乙兩地的棉花中各隨機抽取20根棉花纖維進行統計,結果如下表:(記纖維長度不低于300mm的為“長纖維”,其余為“短纖維”)
纖維長度 | (0,100) | [100,200) | [200,300) | [300,400) | [400,500] |
甲地(根數) | 3 | 4 | 4 | 5 | 4 |
乙地(根數) | 1 | 1 | 2 | 10 | 6 |
(1)由以上統計數據,填寫下面2×2列聯表,并判斷能否在犯錯誤概率不超過0.025的前提下認為“纖維長度與土壤環境有關系”.
甲地 | 乙地 | 總計 | |
長纖維 | |||
短纖維 | |||
總計 |
附:(1) ![]() ;(2)臨界值表;
;(2)臨界值表;
P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(2)現從上述40根纖維中,按纖維長度是否為“長纖維”還是“短纖維”采用分層抽樣的方法抽取8根進行檢測,在這8根纖維中,記乙地“短纖維”的根數為X,求X的分布列及數學期望.
【答案】
(1)9;16;25;11;4;15;20;20;40
(2)由表可知在8根中乙地“短纖維”的根數為 ![]() ,X的可能取值為:0,1,2,3,
,X的可能取值為:0,1,2,3, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
∴X的分布列為:
X | 0 | 1 | 2 | 3 |
P | | | | |
∴ ![]()
【解析】解:(Ⅰ)根據已知數據得到如下2×2列聯表:
甲地 | 乙地 | 總計 | |
長纖維 | 9 | 16 | 25 |
短纖維 | 11 | 4 | 15 |
總計 | 20 | 20 | 40 |
根據2×2列聯表中的數據,可得 ![]()
所以,在犯錯誤概率不超過0.025的前提下認為“纖維長度與土壤環境有關系”.
【考點精析】掌握離散型隨機變量及其分布列是解答本題的根本,需要知道在射擊、產品檢驗等例子中,對于隨機變量X可能取的值,我們可以按一定次序一一列出,這樣的隨機變量叫做離散型隨機變量.離散型隨機變量的分布列:一般的,設離散型隨機變量X可能取的值為x1,x2,.....,xi,......,xn,X取每一個值 xi(i=1,2,......)的概率P(ξ=xi)=Pi,則稱表為離散型隨機變量X 的概率分布,簡稱分布列.


科目:高中數學 來源: 題型:
【題目】已知m>0, ![]() ,
, ![]() .
.
(1) 若p是q的充分不必要條件,求實數m的取值范圍;
(2) 若m=5,“![]() ”為真命題,“
”為真命題,“![]() ”為假命題,求實數x的取值范圍.
”為假命題,求實數x的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知直線l:![]()
![]() 1
1![]() 證明直線l經過定點并求此點的坐標;
證明直線l經過定點并求此點的坐標;
![]() 2
2![]() 若直線l不經過第四象限,求k的取值范圍;
若直線l不經過第四象限,求k的取值范圍;
![]() 3
3![]() 若直線l交x軸負半軸于點A,交y軸正半軸于點B,O為坐標原點,設
若直線l交x軸負半軸于點A,交y軸正半軸于點B,O為坐標原點,設![]() 的面積為S,求S的最小值及此時直線l的方程.
的面積為S,求S的最小值及此時直線l的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在△ABC中,角A,B,C的對邊長分別為a,b,c,且cos2B﹣cos2A=2sinC(sinA﹣sinC).
(1)求角B的大小;
(2)若 ![]() ,求2a+c的取值范圍.
,求2a+c的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=ex﹣ax+a(a∈R),其中e為自然對數的底數.
(1)討論函數y=f(x)的單調性;
(2)函數y=f(x)的圖象與x軸交于A(x1 , 0),B(x2 , 0)兩點,x1<x2 , 點C在函數y=f(x)的圖象上,且△ABC為等腰直角三角形,記 ![]() ,求at﹣(a+t)的值.
,求at﹣(a+t)的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,平面![]() 平面
平面![]() ,四邊形
,四邊形![]() 和
和![]() 是全等的等腰梯形,其中
是全等的等腰梯形,其中![]() ,且
,且![]() ,點
,點![]() 為
為![]() 的中點,點
的中點,點![]() 是
是![]() 的中點.
的中點.
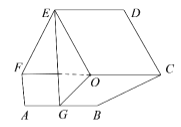
(Ⅰ)求證: ![]() 平面
平面![]() ;
;
(Ⅱ)請在圖中所給的點中找出兩個點,使得這兩點所在的直線與平面![]() 垂直,并給出證明;
垂直,并給出證明;
(Ⅲ)在線段![]() 上是否存在點,使得
上是否存在點,使得![]() 平面
平面![]() ?如果存在,求出
?如果存在,求出![]() 的長度;如果不存在,請說明理由.
的長度;如果不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com