
已知:函數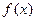 對一切實數
對一切實數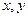 都有
都有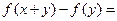
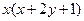 成立,且
成立,且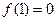 .
.
(1)求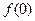 的值。
的值。
(2)求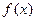 的解析式。
的解析式。
(3)已知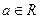 ,設P:當
,設P:當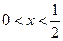 時,不等式
時,不等式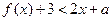 恒成立;Q:當
恒成立;Q:當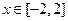 時,
時,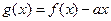 是單調函數。如果滿足P成立的
是單調函數。如果滿足P成立的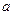 的集合記為
的集合記為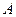 ,滿足Q成立的
,滿足Q成立的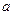 的集合記為
的集合記為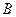 ,求
,求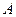 ∩
∩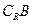 (
(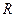 為全集)。
為全集)。
 七星圖書口算速算天天練系列答案
七星圖書口算速算天天練系列答案科目:高中數學 來源: 題型:解答題
本題滿分12分,每小題各4分)
已知函數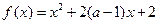 ,
,
(1)若函數 的值域為
的值域為 ,求實數a的值;
,求實數a的值;
(2)若函數 的遞增區間為
的遞增區間為 ,求實數a的值;
,求實數a的值;
(3)若函數 在區間
在區間
 上是增函數,求實數a的取值范圍.
上是增函數,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
.(12分)已知函數 的定義域為
的定義域為 ,且同時滿足:(Ⅰ)對任意
,且同時滿足:(Ⅰ)對任意 ,總有
,總有 ;(Ⅱ)
;(Ⅱ)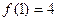 ;(Ⅲ)若
;(Ⅲ)若 ,則有
,則有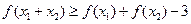
(1)試求 的值;
的值;
(2)試求函數 的最大值;
的最大值;
(3)試證明:當 時,
時, 。
。
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分12分)
已知p:方程x2+mx+1=0有兩個不等的 負實根,q:方程4x2+4(m-2)x+1=0無實根。若p或q為真,p且q為假。求實數m的取值范圍。
負實根,q:方程4x2+4(m-2)x+1=0無實根。若p或q為真,p且q為假。求實數m的取值范圍。
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖,某污水處理廠要在一個矩形污水處理池(ABCD)的池底水平鋪設污水凈化管道(Rt∆FHE,H是直角頂點)來處理污水,管道越長,污水凈化效果越好.設計要求管道的接口H是AB的中點,E,F分別落在線段BC,AD上.已知AB=20米,AD=10 米,記∠BHE=θ.
米,記∠BHE=θ.
(1)試將污水凈化管道的長度L表示為θ的函數,并寫出定義域;
(2)若sinθ+cosθ=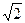 ,求此時管道的長度L;
,求此時管道的長度L;
(3)問:當θ取何值時,污水凈化效果最好?
并求出此時管道的長度.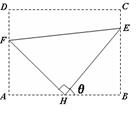
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題13分)某飲料生產企業為了占有更多的市場份額,擬在2010年度進行
一系列促銷活動,經過市場調查和測算,飲料的年銷售量x萬件與年促銷費t萬元間滿足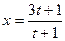 。已知2010年生產飲料的設備折舊
。已知2010年生產飲料的設備折舊 ,維修等固定費用為3 萬元,每生產1萬件
,維修等固定費用為3 萬元,每生產1萬件
飲料需再投入32萬元的生產費用,若將每件飲料的售價定為:其生產成本的150%與平均
每件促銷費的一半之和,則該年生產的飲料正好能銷售完。
(1)將2010年的利潤y(萬元)表示為促銷費t(萬元)的函數;
(2)該企業2010年的促銷費投入多少萬元時,企業的年利潤最大?
(注:利潤=銷售收入—生產 成本—促銷費,生產成本=固定費用+生產費用)
成本—促銷費,生產成本=固定費用+生產費用)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com