【題目】PM2.5是指空氣中直徑小于或等于2.5微米的顆粒物（也稱可入肺顆粒物），為了探究車流量與PM2.5的濃度是否相關，現采集到某城市周一至周五某一時間段車流量與PM2.5濃度的數據如下表：
時間 | 周一 | 周二 | 周三 | 周四 | 周五 |
車流量x（萬輛） | 100 | 102 | 108 | 114 | 116 |
PM2.5的濃度y（微克/立方米） | 78 | 80 | 84 | 88 | 90 |
（1）根據上表數據，用最小二乘法，求出y關于x的線性回歸方程
x
；
（2）若周六同一時間段車流量200萬輛，試根據（1）求出的線性回歸方程，預測此時PM2.5的濃度為多少？
（參考公式：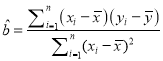
，
；參考數據：
xi＝540，yi＝420）
同步練習強化拓展系列答案科目：高中數學 來源： 題型：
【題目】“有黑掃黑、無黑除惡、無惡治亂”，維護社會穩定和和平發展.掃黑除惡期間，大量違法分子主動投案，某市公安機關對某月連續7天主動投案的人員進行了統計，
表示第
天主動投案的人數，得到統計表格如下：
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 3 | 4 | 5 | 5 | 5 | 6 | 7 |
（1）若與具有線性相關關系，請根據上表提供的數據，用最小二乘法求出關于的線性回歸方程
；
（2）判定變量與之間是正相關還是負相關.（寫出正確答案，不用說明理由）
（3）預測第八天的主動投案的人數（按四舍五入取到整數）.
參考公式：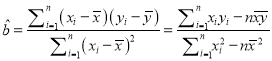
， 
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】為了讓稅收政策更好的為社會發展服務,國家在修訂《中華人民共和國個人所得稅法》之后，發布了《個人所得稅專項附加扣除暫行辦法》，明確“專項附加扣除”就是子女教育、繼續教育大病醫療、住房貸款利息、住房租金贈養老人等費用，并公布了相應的定額扣除標準，決定自2019年1月1日起施行，某機關為了調查內部職員對新個稅方案的滿意程度與年齡的關系，通過問卷調查，整理數據得如下2×2列聯表：
40歲及以下 | 40歲以上 | 合計 | |
基本滿意 | 15 | 10 | 25 |
很滿意 | 25 | 30 | 55 |
合計 | 40 | 40 | 80 |
（1）根據列聯表,能否有85%的把握認為滿意程度與年齡有關?
（2）若已經在滿意程度為“基本滿意”的職員中用分層抽樣的方式選取了5名職員,現從這5名職員中隨機選取3名進行面談求面談的職員中恰有2名年齡在40歲及以下的概率.
附：
，其中
.
參考數據：
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】青島二中高一高二高三三個年級數學MT的學生人數分別為240人，240人，120人，現采用分層抽樣的方法從中抽取5名同學參加團隊內部舉辦的趣味數學比賽，再從5位同學中選出2名一等獎記A＝“兩名一等獎來自同一年級”，則事件A的概率為_____．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，已知橢圓C：
1（a＞b＞0）的右焦點為F，A（2，0）是橢圓的右頂點，過F且垂直于x軸的直線交橢圓于P，Q兩點，且|PQ|＝3．
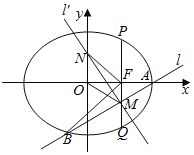
（1）求橢圓的方程；
（2）過點A的直線l與橢圓交于另一點B，垂直于l的直線l′與直線l交于點M，與y軸交于點N，若FB⊥FN且|MO|＝|MA|，求直線l的方程．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖1，在邊長為3的菱形
中，已知
，且
.將梯形
沿直線
折起，使
平面
，如圖2，
分別是
上的點.
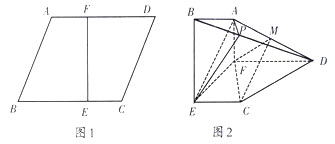
（1）若平面
平面
，求
的長；
（2）是否存在點
，使直線
與平面
所成的角是
？若存在，求出
的值；若不存在，請說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】根據下圖給出的2000年至2016年我國實際利用外資情況，以下結論正確的是
A. 2000年以來我國實際利用外資規模與年份負相關
B. 2010年以來我國實際利用外資規模逐年增加
C. 2008年我國實際利用外資同比增速最大
D. 2010年以來我國實際利用外資同比增速最大
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
