【題目】橢圓
：
的左，右焦應分別是
，
，離心率為
，過且垂直于
軸的直線被橢圓截得的線段長為1.
（1）求橢圓的方程；
（2）已知直線
：
與橢圓切于點
，直線
平行于
，與橢圓交于不同的兩點
、
，且與直線交于點
.證明：存在常數
，使得
，并求的值；
（3）點
是橢圓上除長軸端點外的任一點，連接
，
，設
后的角平分線
交的長軸于點
，求
的取值范圍.
新思維寒假作業系列答案科目：高中數學 來源： 題型：
【題目】某公司制定了一個激勵銷售人員的獎勵方案:對于每位銷售人員,均以10萬元為基數,若銷售利潤沒超出這個基數,則可獲得銷售利潤的5%的獎金;若銷售利潤超出這個基數(超出的部分是a萬元),則可獲得
萬元的獎金.記某位銷售人員獲得的獎金為y(單位:萬元),其銷售利潤為x(單位:萬元).
(1)寫出這位銷售人員獲得的獎金y與其銷售利潤x之間的函數關系式;
(2)如果這位銷售人員獲得了
萬元的獎金,那么他的銷售利潤是多少萬元?
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某學校高二年級的第二學期，因某學科的任課教師王老師調動工作，于是更換了另一名教師趙老師繼任.第二學期結束后從全學年的該門課的學生考試成績中用隨機抽樣的方法抽取了容量為50的樣本，用莖葉圖表示如下：
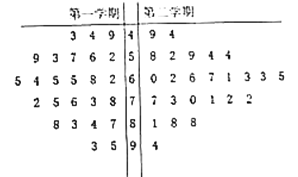
學校秉持均衡發展、素質教育的辦學理念，對教師的教學成績實行績效考核，績效考核方案規定：每個學期的學生成績中與其中位數相差在
范圍內（含）的為合格，此時相應的給教師賦分為1分；與中位數之差大于10的為優秀，此時相應的給教師賦分為2分；與中位數之差小于-10的為不合格，此時相應的給教師賦分為-1分.
（Ⅰ）問王老師和趙老師的教學績效考核成績的期望值哪個大？
（Ⅱ）是否有
的把握認為“學生成績取得優秀與更換老師有關”.
附：
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】等比數列{an}的各項均為正數，且2a1＋3a2＝1， 
＝9a2a6.
(1)求數列{an}的通項公式；
(2)設bn＝log3a1＋log3a2＋…＋log3an，求數列
的前n項和．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
，把函數
的圖象向右平移
個單位，再把圖象上各點的橫坐標縮小到原來的一半，縱坐標不變，得到函數
的圖象，當
時，方程
恰有兩個不同的實根，則實數
的取值范圍為（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在如圖所示的幾何體中，四邊形
是菱形，
是矩形，
，
，
， 
，
為
的中點.
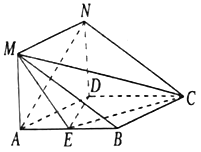
（1）平面
平面
（2）在線段
上是否存在點
，使二面角
的大小為
？若存在，求出
的長度；若不存在，請說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設橢圓
的中心在坐標原點
，其中一個焦點為圓
的圓心，右頂點是圓
與
軸的一個交點.已知橢圓與直線
相交于
、
兩點，延長
與橢圓交于點
.
（1）求橢圓的方程；
（2）求
面積的最大值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】一年之計在于春，一日之計在于晨，春天是播種的季節，是希望的開端.某種植戶對一塊地的
個坑進行播種，每個坑播3粒種子，每粒種子發芽的概率均為
，且每粒種子是否發芽相互獨立.對每一個坑而言，如果至少有兩粒種子發芽，則不需要進行補播種，否則要補播種.
（1）當
取何值時，有3個坑要補播種的概率最大？最大概率為多少？
（2）當
時，用
表示要補播種的坑的個數，求的分布列與數學期望.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
