
【題目】紀念幣是一個國家為紀念國際或本國的政治、歷史,文化等方面的重大事件、杰出人物、名勝古跡、珍稀動植物、體育賽事等而發(fā)行的法定貨幣.我國在1984年首次發(fā)行紀念幣,目前已發(fā)行了115套紀念幣,這些紀念幣深受郵幣愛好者的喜愛與收藏.2019年發(fā)行的第115套紀念幣“雙遺產(chǎn)之泰山幣”是目前為止發(fā)行的第一套異形幣,因為這套紀念幣的多種特質,更加受到愛好者追捧.某機構為調查我國公民對紀念幣的喜愛態(tài)度,隨機選了某城市某小區(qū)的50位居民調查,調查結果統(tǒng)計如下:
喜愛 | 不喜愛 | 合計 | |
年齡不大于40歲 | 24 | ||
年齡大于40歲 | 20 | ||
合計 | 22 | 50 |
(1)根據(jù)已有數(shù)據(jù),把表格數(shù)據(jù)填寫完整,判斷能否在犯錯誤的概率不超過![]() 的前提下認為不同年齡與紀念幣的喜愛無關?
的前提下認為不同年齡與紀念幣的喜愛無關?
(2)已知在被調查的年齡不大于40歲的喜愛者中有5名男性,其中3位是學生,現(xiàn)從這5名男性中隨機抽取2人,求至多有1位學生的概率.
附: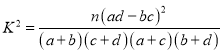 ,
,![]() .
.
| 0.100 | 0.050 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
【答案】(1)表見解析,犯錯誤的概率不超過![]() 的條件下認為不同年齡與紀念幣的喜愛無關;(2)
的條件下認為不同年齡與紀念幣的喜愛無關;(2)![]()
【解析】
(1)根據(jù)條件,列出列聯(lián)表,填上對應的數(shù)據(jù),把求得的數(shù)據(jù)代入求![]() 的公式求出值,并判斷即可得到結論;
的公式求出值,并判斷即可得到結論;
(2)利用列舉法確定基本事件,即可求出概率.
喜愛 | 不喜愛 | 合計 | |
年齡不大于40歲 | 8 | 16 | 24 |
年齡大于40歲 | 20 | 6 | 26 |
合計 | 28 | 22 | 50 |
(1)![]()
![]() .
.
∴能在犯錯誤的概率不超過![]() 的條件下認為不同年齡與紀念幣的喜愛無關.
的條件下認為不同年齡與紀念幣的喜愛無關.
(2)記不大于40歲的5位喜愛者中的3位學生記為![]() ,
,![]() ,
,![]() ,非學生記為
,非學生記為![]() ,
,![]() ,
,
則從5人中任取2人,共有![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 共10種結果.
共10種結果.
其中至多有1位學生的有7種,∴至多有1位學生的概率![]() .
.


 靈星計算小達人系列答案
靈星計算小達人系列答案 孟建平錯題本系列答案
孟建平錯題本系列答案科目:高中數(shù)學 來源: 題型:
【題目】曲線![]() 上動點
上動點![]() 到定點
到定點![]() 與定直線
與定直線![]() 的距離之比為常數(shù)
的距離之比為常數(shù)![]() ;
;
(1)求曲線![]() 的軌跡方程;
的軌跡方程;
(2)設圓心為![]() 的圓
的圓![]()
![]() 與曲線
與曲線![]() 交于點
交于點![]() 與點
與點![]() ,求
,求![]() 的最小值,并求此時圓
的最小值,并求此時圓![]() 的方程;
的方程;
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,在三棱錐![]() 中,平面
中,平面![]() 平面
平面![]() ,
,![]() 和
和![]() 均是等腰直角三角形,
均是等腰直角三角形,![]() ,
,![]() ,
,![]() 、
、![]() 分別為
分別為![]() 、
、![]() 的中點.
的中點.
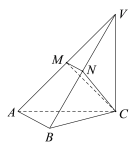
(Ⅰ)求證:![]() 平面
平面![]() ;
;
(Ⅱ)求證:![]() ;
;
(Ⅲ)求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<![]() )的部分圖象如圖所示.
)的部分圖象如圖所示.
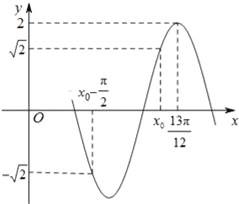
(Ⅰ)寫出函數(shù)f(x)的解析式及x0的值;
(Ⅱ)求函數(shù)f(x)在區(qū)間[﹣![]() ,
,![]() ]上的最大值與最小值.
]上的最大值與最小值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】![]() 是定義在
是定義在![]() 上的奇函數(shù),對
上的奇函數(shù),對![]() ,均有
,均有![]() ,已知當
,已知當![]() 時,
時, ![]() ,則下列結論正確的是( )
,則下列結論正確的是( )
A. ![]() 的圖象關于
的圖象關于![]() 對稱 B.
對稱 B. ![]() 有最大值1
有最大值1
C. ![]() 在
在![]() 上有5個零點 D. 當
上有5個零點 D. 當![]() 時,
時, ![]()
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() ,如果存在給定的實數(shù)對
,如果存在給定的實數(shù)對![]() ,使得
,使得![]() 恒成立,則稱
恒成立,則稱![]() 為“
為“![]() 函數(shù)”;
函數(shù)”;
(1)判斷函數(shù)![]() ,
,![]() 是否是“
是否是“![]() 函數(shù)”;
函數(shù)”;
(2)若![]() 是一個“
是一個“![]() 函數(shù)”,求出所有滿足條件的有序實數(shù)對
函數(shù)”,求出所有滿足條件的有序實數(shù)對![]() ;
;
(3)若定義域為![]() 的函數(shù)
的函數(shù)![]() 是“
是“![]() 函數(shù)”,且存在滿足條件的有序實數(shù)對
函數(shù)”,且存在滿足條件的有序實數(shù)對![]() 和
和![]() ,當
,當![]() 時,
時,![]() 的值域為
的值域為![]() ,求當
,求當![]() 時
時![]() 的值域;
的值域;
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
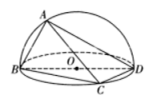
【題目】如圖,已知![]() 是圓
是圓![]() 的直徑,
的直徑,![]() ,
,![]() 在圓上且分別在
在圓上且分別在![]() 的兩側,其中
的兩側,其中![]() ,
,![]() .現(xiàn)將其沿
.現(xiàn)將其沿![]() 折起使得二面角
折起使得二面角![]() 為直二面角,則下列說法不正確的是( )
為直二面角,則下列說法不正確的是( )
A.![]() ,
,![]() ,
,![]() ,
,![]() 在同一個球面上
在同一個球面上
B.當![]() 時,三棱錐
時,三棱錐![]() 的體積為
的體積為![]()
C.![]() 與
與![]() 是異面直線且不垂直
是異面直線且不垂直
D.存在一個位置,使得平面![]() 平面
平面![]()
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在貫徹中共中央、國務院關于精準扶貧政策的過程中,某單位在某市定點幫扶某村![]() 戶貧困戶.為了做到精準幫扶,工作組對這
戶貧困戶.為了做到精準幫扶,工作組對這![]() 戶村民的年收入情況、危舊房情況、患病情況等進行調查,并把調查結果轉化為各戶的貧困指標
戶村民的年收入情況、危舊房情況、患病情況等進行調查,并把調查結果轉化為各戶的貧困指標![]() .將指標
.將指標![]() 按照
按照![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分成五組,得到如圖所示的頻率分布直方圖.規(guī)定若
分成五組,得到如圖所示的頻率分布直方圖.規(guī)定若![]() ,則認定該戶為“絕對貧困戶”,否則認定該戶為“相對貧困戶”;當
,則認定該戶為“絕對貧困戶”,否則認定該戶為“相對貧困戶”;當![]() 時,認定該戶為“亟待幫住戶”.工作組又對這
時,認定該戶為“亟待幫住戶”.工作組又對這![]() 戶家庭的受教育水平進行評測,家庭受教育水平記為“良好”與“不好”兩種.
戶家庭的受教育水平進行評測,家庭受教育水平記為“良好”與“不好”兩種.

(1)完成下面的列聯(lián)表,并判斷是否有![]() 的把握認為絕對貧困戶數(shù)與受教育水平不好有關:
的把握認為絕對貧困戶數(shù)與受教育水平不好有關:
受教育水平良好 | 受教育水平不好 | 總計 | |
絕對貧困戶 |
| ||
相對貧困戶 |
| ||
總計 |
|
(2)上級部門為了調查這個村的特困戶分布情況,在貧困指標處于![]() 的貧困戶中,隨機選取兩戶,用
的貧困戶中,隨機選取兩戶,用![]() 表示所選兩戶中“亟待幫助戶”的戶數(shù),求
表示所選兩戶中“亟待幫助戶”的戶數(shù),求![]() 的分布列和數(shù)學期望
的分布列和數(shù)學期望![]() .
.
附: ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com