
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,兩焦點與短軸的一個端點的連線構(gòu)成的三角形面積為
,兩焦點與短軸的一個端點的連線構(gòu)成的三角形面積為![]() .
.
(Ⅰ)求橢圓C的方程;
(Ⅱ)設(shè)與圓O:![]() 相切的直線l交橢圓C于A,B兩點(O為坐標原點),求△AOB面積的最大值。
相切的直線l交橢圓C于A,B兩點(O為坐標原點),求△AOB面積的最大值。
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() .
.
【解析】
(Ⅰ)利用橢圓的離心率為![]() ,兩焦點與短軸的一個端點的連線構(gòu)成的三角形面積為
,兩焦點與短軸的一個端點的連線構(gòu)成的三角形面積為![]() ,建立方程,即可求橢圓C的方程;
,建立方程,即可求橢圓C的方程;
(Ⅱ)對直線AB的斜率分類討論,設(shè)直線AB的方程為![]() ,利用相切可得
,利用相切可得![]() ,與橢圓聯(lián)立,利用韋達定理可以表示
,與橢圓聯(lián)立,利用韋達定理可以表示![]() ,利用均值不等式求出最值即可得到△AOB面積的最大值
,利用均值不等式求出最值即可得到△AOB面積的最大值
解:(I)由題設(shè):![]() ,
,
解得![]()
∴橢圓C的方程為![]()
(Ⅱ).設(shè)![]()
1.當AB![]() x軸時,
x軸時,![]()
2.當AB與x軸不垂直時,設(shè)直線AB的方程為![]()
由已知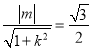 ,得
,得![]()
把![]() 代入橢圓方程消去y,
代入橢圓方程消去y,
整理得![]() ,
,
有![]()
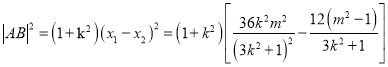 ,
,
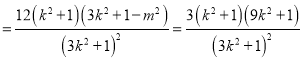 ,
,
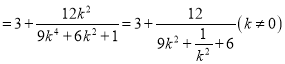 ,
,
![]() ,
,
當且僅當![]() ,即
,即![]() 時等號成立.
時等號成立.
當![]() 時,
時,![]()
綜上所述![]() ,從而△AOB面積的最大值為
,從而△AOB面積的最大值為![]()


科目:高中數(shù)學(xué) 來源: 題型:
【題目】為支援邊遠地區(qū)教育事業(yè)的發(fā)展,現(xiàn)有5名師范大學(xué)畢業(yè)生主動要求赴西部某地區(qū)三所不同的學(xué)校去支教,每個學(xué)校至少去1人,甲、乙不能安排在同一所學(xué)校,則不同的安排方法有( )
A.180種B.150種C.90種D.114種
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知雙曲線![]() 的右頂點為
的右頂點為![]() , 以
, 以![]() 為圓心的圓與雙曲線
為圓心的圓與雙曲線![]() 的某一條漸近線交于兩點
的某一條漸近線交于兩點![]() .若
.若![]() ,且
,且![]() (其中
(其中![]() 為原點),則雙曲線
為原點),則雙曲線![]() 的離心率為( )
的離心率為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓C:![]() 上頂點為A,右頂點為B,離心率
上頂點為A,右頂點為B,離心率![]() ,O為坐標原點,原點到直線AB的距離為
,O為坐標原點,原點到直線AB的距離為![]() .
.
(1)求橢圓C的標準方程;
(2)直線![]() 與橢圓C相交于E、F兩不同點,若橢圓C上一點P滿足
與橢圓C相交于E、F兩不同點,若橢圓C上一點P滿足![]() .求△EPF面積的最大值及此時的
.求△EPF面積的最大值及此時的![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)函數(shù)![]() .
.
(1)討論函數(shù)![]() 的單調(diào)性;
的單調(diào)性;
(2)如果對所有的![]() ≥1,都有
≥1,都有![]() ≤
≤![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某消費者協(xié)會在3月15號舉行了以“攜手共治,暢享消費”為主題的大型宣傳咨詢服務(wù)活動,著力提升消費者維權(quán)意識.組織方從參加活動的1000名群眾中隨機抽取n名群眾,按他們的年齡分組:第1組![]() ,第2組
,第2組![]() ,第3組
,第3組![]() ,第4組
,第4組![]() ,第5組
,第5組![]() ,其中第1組
,其中第1組![]() 有6人,得到的頻率分布直方圖如圖所示.
有6人,得到的頻率分布直方圖如圖所示.
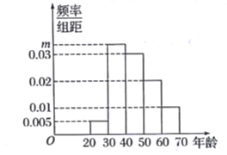
(1)求m,n的值,并估計抽取的n名群眾中年齡在![]() 的人數(shù);
的人數(shù);
(2)已知第1組群眾中男性有2人,組織方要從第1組中隨機抽取3名群眾組成維權(quán)志愿者服務(wù)隊,求至少有兩名女生的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)全集U=R,集合A={x|1≤x<4},B={x|2a≤x<3-a}.
(1)若a=-2,求B∩A,B∩(UA);(2)若A∪B=A,求實數(shù)a的取值范圍.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com