Question

【題目】如下圖,是長方形，平面平面，且是的中點.

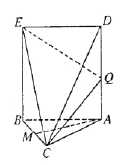
(Ⅰ) 求證：平面；

(Ⅱ) 求三棱錐的體積；

（Ⅲ）若點是線段上的一點，且平面平面,求線段的長.

Answer 1

【答案】（Ⅰ）詳見解析；（Ⅱ）24；（Ⅲ）3.

【解析】試題分析：（Ⅰ）由平面平面，得到平面，即，又因為，進而證明平面；（Ⅱ）根據（Ⅰ）知道就是三棱錐的高，又因為，所以；（Ⅲ）根據平面，過做的平行線交與點，則有平面,進而可以得到平面平面，確定線段的長度，所以在平面內作交于點.

試題解析：（Ⅰ）證明：平面平面，平面平面平面，

平面，又平面，

.

又是的中點，

，又平面平面

平面.

（Ⅱ）解：由（Ⅰ）知，平面.

在中，，

又

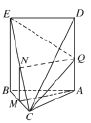
（Ⅲ）證明：在平面內作交于點.

平面平面，平面平面，

平面，又平面.

.

與共面，設該平面為，

是長方形，，

又平面平面，

平面，又平面，

，又，

四邊形是平行四方形.

.

，

，又是的中點.

，

.