
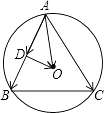
【題目】在△ABC中,內角A,B,C的對邊分別為a,b,c,已知2acosB=2c﹣b,若O是△ABC外接圓的圓心,且 ![]() ,則m= .
,則m= .
【答案】![]()
【解析】解:△ABC中,2acosB=2c﹣b, ∴2a ![]() =2c﹣b,
=2c﹣b,
∴b2+c2﹣a2=bc,
∴cosA= ![]() =
= ![]() =
= ![]() ;
;
又A∈(0,π),∴A= ![]() ;
;
由O是△ABC外接圓的圓心,取AB中點D,
則有 ![]() =
= ![]() +
+ ![]() ,如圖所示;
,如圖所示;
∴ ![]()
![]() +
+ ![]()
![]() =m
=m ![]() =m(
=m( ![]() +
+ ![]() );
);
由 ![]() ⊥
⊥ ![]() 得
得 ![]()
![]() =0,
=0,
∴ ![]()
![]()
![]() +
+ ![]()
![]()
![]() =m(
=m( ![]() +
+ ![]() )
) ![]()
=m ![]()
![]() +m
+m ![]()
![]() =
= ![]() m
m ![]() ,
,
即 ![]() c2+
c2+ ![]() bccosA=
bccosA= ![]() mc2;
mc2;
由正弦定理化簡得 ![]() sin2C+
sin2C+ ![]() sinBsinCcosA=
sinBsinCcosA= ![]() msin2C,
msin2C,
由sinC≠0,兩邊同時除以sinC得:cosB+cosAcosC= ![]() msinC,
msinC,
∴ ![]() m=
m= ![]()
= ![]()
= ![]()
=sinA=sin ![]() =
= ![]() ,
,
解得m= ![]() .
.
所以答案是: ![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】
一個盒子里裝有三張卡片,分別標記有數字1,2,3,這三張卡片除標記的數字外完全相同.隨機有放回地抽取3次,每次抽取1張,將抽取的卡片上的數字依次記為![]() .
.
(1)求“抽取的卡片上的數字滿足![]() ”的概率;
”的概率;
(2)求“抽取的卡片上的數字![]() 不完全相同”的概率.
不完全相同”的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某折疊餐桌的使用步驟如圖所示,有如圖檢查項目:
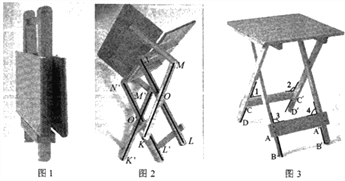
項目①:折疊狀態下(如圖1),檢查四條桌腿長相等;
項目②:打開過程中(如圖2),檢查![]() ;
;
項目③:打開過程中(如圖2),檢查![]() ;
;
項目④:打開后(如圖3),檢查![]() ;
;
項目⑤:打開后(如圖3),檢查![]() .
.
在檢查項目的組合中,可以正確判斷“桌子打開之后桌面與地面平行的是”( )
A. ①②③ B. ②③④ C. ②④⑤ D. ③④⑤
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一戶居民根據以往的月用電量情況,繪制了月用電量的頻率分布直方圖(月用電量都在25度到325度之間)如圖所示.將月用電量落入該區間的頻率作為概率.若每月的用電量在200度以內(含200度),則每度電價0.5元,若每月的用電量超過200度,則超過的部分每度電價0.6元.記![]() (單位:度,
(單位:度,![]() )為該用戶下個月的用電量,
)為該用戶下個月的用電量,![]() (單位:元)為下個月所繳納的電費.
(單位:元)為下個月所繳納的電費.
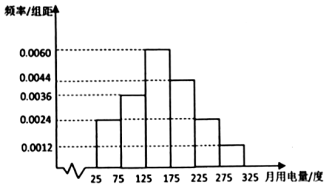
(1)估計該用戶的月用電量的平均值(同一組中的數據用該組區間的中點值作代表);
(2)將![]() 表示為
表示為![]() 的函數;
的函數;
(3)根據直方圖估計下個月所繳納的電費![]() 的概率.
的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】
有甲、乙、丙、丁四名網球運動員,通過對過去戰績的統計,在一場比賽中,甲對乙、丙、丁取勝的概率分別為![]() .
.
(Ⅰ)若甲和乙之間進行三場比賽,求甲恰好勝兩場的概率;
(Ⅱ)若四名運動員每兩人之間進行一場比賽,設甲獲勝場次為![]() ,求隨機變量
,求隨機變量![]() 的分布列及期望
的分布列及期望![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】是否存在一個等比數列{an}同時滿足下列三個條件:①a1+a6=11且a3a4= ![]() ;②an+1>an(n∈N*);③至少存在一個m(m∈N*且m>4),使得
;②an+1>an(n∈N*);③至少存在一個m(m∈N*且m>4),使得 ![]() am﹣1 , am2 , am+1+
am﹣1 , am2 , am+1+ ![]() 依次構成等差數列?若存在,求出通項公式;若不存在,說明理由.
依次構成等差數列?若存在,求出通項公式;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知命題![]() “存在
“存在![]() ”,命題
”,命題![]() :“曲線
:“曲線![]() 表示焦點在
表示焦點在![]() 軸上的橢圓”,命題
軸上的橢圓”,命題![]() “曲線
“曲線![]() 表示雙曲線”
表示雙曲線”
(1)若“![]() 且
且![]() ”是真命題,求實數
”是真命題,求實數![]() 的取值范圍;
的取值范圍;
(2)若![]() 是
是![]() 的必要不充分條件,求實數
的必要不充分條件,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知過原點的動直線![]() 與圓
與圓![]() 相交于不同的兩點
相交于不同的兩點![]() .
.
(1)求線段![]() 的中點
的中點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(2)是否存在實數![]() ,使得直線
,使得直線![]() 與曲線
與曲線![]() 只有一個交點?若存在,求出
只有一個交點?若存在,求出![]() 的取值范圍;若不存在,請說明理由.
的取值范圍;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com