
【題目】《中華人民共和國道路交通安全法》第47條規定:機動車行經人行橫道時,應當減速慢行;遇到行人正在通過人行橫道,應當停車讓行,俗稱“禮讓斑馬線”.下表是某十字路口監控設備所抓拍的6個月內駕駛員不“禮讓斑馬線”行為的統計數據:
月份 | 1 | 2 | 3 | 4 | 5 | 6 |
不“禮讓斑馬線”駕駛員人數 | 120 | 105 | 100 | 85 | 90 | 80 |
(Ⅰ)請根據表中所給前5個月的數據,求不“禮讓斑馬線”的駕駛員人數![]() 與月份
與月份![]() 之間的回歸直線方程
之間的回歸直線方程![]() ;
;
(Ⅱ)若該十字路口某月不“禮讓斑馬線”駕駛員人數的實際人數與預測人數之差小于5,則稱該十字路口“禮讓斑馬線”情況達到“理想狀態”.試根據(Ⅰ)中的回歸直線方程,判斷6月份該十字路口“禮讓斑馬線”情況是否達到“理想狀態”?
(Ⅲ)若從表中3、4月份分別選取4人和2人,再從所選取的6人中任意抽取2人進行交規調查,求抽取的兩人恰好來自同一月份的概率.
參考公式:
 ,
,![]() .
.
【答案】(Ⅰ)![]() ;(Ⅱ)見解析;(Ⅲ)
;(Ⅱ)見解析;(Ⅲ)![]()
【解析】試題分析:(Ⅰ)依題意![]() ,
,![]() ,根據公式求得
,根據公式求得![]() 的值,即可得到回歸直線方程;
的值,即可得到回歸直線方程;
(Ⅱ)由(Ⅰ)得當![]() 時,
時,![]() ,即可根據題意作出判斷結論;
,即可根據題意作出判斷結論;
(Ⅲ)設3月份選取的4位駕駛的編號分別為:![]() ,
,![]() ,
,![]() ,
,![]() ,從4月份選取的2位駕駛員的編號分別為
,從4月份選取的2位駕駛員的編號分別為![]() ,
,![]() ,列出基本事件的總體,用古典概型及概率計算公式,即可求解概率.
,列出基本事件的總體,用古典概型及概率計算公式,即可求解概率.
試題解析:
(Ⅰ)依題意![]() ,
,![]() ,
,
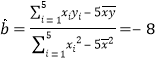 ,
,![]() ,
,
∴![]() 關于
關于![]() 的線性回歸方程為:
的線性回歸方程為:![]() .
.
(Ⅱ)由(Ⅰ)得![]() ,當
,當![]() 時,
時,![]() .
.
![]() ,故6月份該十字路口“禮讓斑馬線”情況達到“理想狀態”.
,故6月份該十字路口“禮讓斑馬線”情況達到“理想狀態”.
(Ⅲ)設3月份選取的4位駕駛的編號分別為:![]() ,
,![]() ,
,![]() ,
,![]() ,從4月份選取的2位駕駛員的編號分別為
,從4月份選取的2位駕駛員的編號分別為![]() ,
,![]() ,從這6人中任抽兩人包含以下基本事件:
,從這6人中任抽兩人包含以下基本事件:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 共15個基本事件,其中兩個恰好來自同一月份的包含7個基本事件,
共15個基本事件,其中兩個恰好來自同一月份的包含7個基本事件,
∴所求概率![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐P﹣ABCD中,PA⊥平面ABCD,底面ABCD是菱形,點O是對角線AC與BD的交點,M是PD的中點.

(1)求證:OM∥平面PAB;
(2)求證:平面PBD⊥平面PAC.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我國南北朝數學家何承天發明的“調日法”是程序化尋求精確分數來表示數值的算法,其理論依據是:設實數![]() 的不足近似值和過剩近似值分別為
的不足近似值和過剩近似值分別為![]() 和
和![]()
![]() ,則
,則![]() 是
是![]() 的更為精確的近似值.
的更為精確的近似值.
我們知道![]() ,我國早在《周髀算經》中就有“周三徑一”的古率記載,《隋書律歷志》有如下記載:“南徐州從事史祖沖之更開密法,以圓徑一億為丈,圓周盈數三丈一尺四寸一分五厘九毫二秒七忽,肭數三丈一尺四寸一分五厘九毫二秒六忽,正數在盈肭二限之間。密率:圓徑一百一十三,圓周三百五十五。約率,圓徑七,周二十二”,這一記錄指出了祖沖之關于圓周率的兩大貢獻:其一是求得圓周率
,我國早在《周髀算經》中就有“周三徑一”的古率記載,《隋書律歷志》有如下記載:“南徐州從事史祖沖之更開密法,以圓徑一億為丈,圓周盈數三丈一尺四寸一分五厘九毫二秒七忽,肭數三丈一尺四寸一分五厘九毫二秒六忽,正數在盈肭二限之間。密率:圓徑一百一十三,圓周三百五十五。約率,圓徑七,周二十二”,這一記錄指出了祖沖之關于圓周率的兩大貢獻:其一是求得圓周率![]() ;其二是得到
;其二是得到![]() 的兩個近似分數即:約率為22/7,密率為355/113,他算出的
的兩個近似分數即:約率為22/7,密率為355/113,他算出的![]() 的8位可靠數字,不但在當時是最精密的圓周率,而且保持世界紀錄一千多年,他對
的8位可靠數字,不但在當時是最精密的圓周率,而且保持世界紀錄一千多年,他對![]() 的研究真可謂“運籌于帷幄之中,決勝于千年之外”,祖沖之是我國古代最有影響的數學家之一,莫斯科大學走廊里有其塑像,1959年10月,原蘇聯通過“月球3”號衛星首次拍下月球背面照片后,就以祖沖之命名一個環形山,其月面坐標是:東經148度,北緯17度.
的研究真可謂“運籌于帷幄之中,決勝于千年之外”,祖沖之是我國古代最有影響的數學家之一,莫斯科大學走廊里有其塑像,1959年10月,原蘇聯通過“月球3”號衛星首次拍下月球背面照片后,就以祖沖之命名一個環形山,其月面坐標是:東經148度,北緯17度.
縱橫古今,關于![]() 值的研究,經歷了古代試驗法時期、幾何法時期、分析法時期、蒲豐或然性試驗方法時期、計算機時期,己知
值的研究,經歷了古代試驗法時期、幾何法時期、分析法時期、蒲豐或然性試驗方法時期、計算機時期,己知![]() ,試以上述
,試以上述![]() 的不足近似值
的不足近似值![]() 和過剩近似值
和過剩近似值![]() 為依據,那么使用兩次“調日法”后可得
為依據,那么使用兩次“調日法”后可得![]() 的近似分數為____________
的近似分數為____________
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】國家放開計劃生育政策,鼓勵一對夫婦生育2個孩子.在某地區的100000對已經生育了一胎夫婦中,進行大數據統計得,有100對第一胎生育的是雙胞胎或多胞胎,其余的均為單胞胎.在這99900對恰好生育一孩的夫婦中,男方、女方都愿意生育二孩的有50000對,男方愿意生育二孩女方不愿意生育二孩的有![]() 對,男方不愿意生育二孩女方愿意生育二孩的有
對,男方不愿意生育二孩女方愿意生育二孩的有![]() 對,其余情形有
對,其余情形有![]() 對,且
對,且![]() .現用樣本的頻率來估計總體的概率.
.現用樣本的頻率來估計總體的概率.
(1)說明“其余情形”指何種具體情形,并求出![]() ,
,![]() ,
,![]() 的值;
的值;
(2)該地區為進一步鼓勵生育二孩,實行貼補政策:凡第一胎生育了一孩的夫婦一次性貼補5000元,第一胎生育了雙胞胎或多胞胎的夫婦只有一次性貼補15000元.第一胎已經生育了一孩再生育了二孩的夫婦一次性再貼補20000元.這種補貼政策直接提高了夫婦生育二孩的積極性:原先男方或女方中只有一方愿意生育二孩的夫婦現在都愿意生育二孩,但原先男方、女方都不愿意生育二孩的夫婦仍然不愿意生育二孩.設![]() 為該地區的一對夫婦享受的生育貼補,求
為該地區的一對夫婦享受的生育貼補,求![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列![]() 中,
中,![]() ,點
,點![]() 在直線
在直線![]() 上,其中
上,其中![]() .
.
(1)令![]() ,求證數列
,求證數列![]() 是等比數列;
是等比數列;
(2)求數列![]() 的通項;
的通項;
(3)設![]() 、
、![]() 分別為數列
分別為數列![]() 、
、![]() 的前
的前![]() 項和是否存在實數
項和是否存在實數![]() ,使得數列
,使得數列![]() 為等差數列?若存在,試求出
為等差數列?若存在,試求出![]() ,若不存在,則說明理由.
,若不存在,則說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】國慶期間,一位游客來到某旅游城市,這里有甲、乙、丙三個著名的旅游景點,若這位游客游覽這三個景點的概率分別是![]() ,且客人是否游覽哪個景點互不影響,設
,且客人是否游覽哪個景點互不影響,設![]() 表示客人離開該城市時游覽的景點數與沒有游覽的景點數之差的絕對值.
表示客人離開該城市時游覽的景點數與沒有游覽的景點數之差的絕對值.
(Ⅰ)求![]() 的分布列和數學期望;
的分布列和數學期望;
(Ⅱ)記“![]() 時,不等式
時,不等式![]() 恒成立”為事件
恒成立”為事件![]() ,求事件
,求事件![]() 發生的概率.
發生的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(12分)
煉鋼是一個氧化降碳的過程,由于鋼水含碳量的多少直接影響冶煉時間的長短,因此必須掌握鋼水含碳量和冶煉時間的關系.現已測得爐料熔化完畢時鋼水的含碳量x與冶煉時間y(從爐料熔化完畢到出鋼的時間)的一組數據,如下表所示:

(1)據統計表明,![]() 之間具有線性相關關系,請用相關系數r加以說明(
之間具有線性相關關系,請用相關系數r加以說明(![]()
![]() ,則認為y與x有較強的線性相關關系,否則認為沒有較強的線性相關關系,r精確到0.001);
,則認為y與x有較強的線性相關關系,否則認為沒有較強的線性相關關系,r精確到0.001);
(2)建立y關于x的回歸方程(回歸系數的結果精確到0.01);
(3)根據(2)中的結論,預測鋼水含碳量為160個0.01%的冶煉時間.
參考公式:回歸方程![]() 中斜率和截距的最小二乘估計分別為
中斜率和截距的最小二乘估計分別為 ,
,
![]() ,相關系數
,相關系數
參考數據: ,
,
![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】中國有個名句“運籌帷幄之中,決勝千里之外.”其中的“籌”原意是指《孫子算經》中記載的算籌,古代是用算籌來進行計算,算籌是將幾寸長的小竹棍擺在平面上進行運算,算籌的擺放形式有縱橫兩種形式,如下表
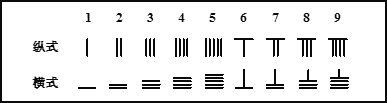
表示一個多位數時,像阿拉伯計數一樣,把各個數位的數碼從左到右排列,但各位數碼的籌式需要縱橫相間,個位,百位,萬位數用縱式表示,十位,千位,十萬位用橫式表示,以此類推, 例如6613用算籌表示就是:![]() ,則26337用算籌可表示為( )
,則26337用算籌可表示為( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com