【題目】已知向量 
=（cosx，sinx）， 
=（ 
sinx，sinx），x∈R設函數f（x）= 
﹣ 
（1）求函數f（x）的最小正周期；
（2）求函數f（x）在[0， 
]上的最大值和最小值．
【答案】
（1）解：由向量 
=（cosx，sinx）， 
=（ 
sinx，sinx），x∈R，
得f（x）= 
﹣ 
= 
= 
．
∴函數f（x）的最小正周期T= 
；
（2）解：當x∈[0， 
]時， 
，
由正弦曲線y=sinx在[ 
， 
]上的圖象可知
當 
即 
時f（x）取最大值1．
當 
即x=0時f（x）取最小值 
．
函數f（x）在[0， ]上的最大值和最小值分別為1， ．
【解析】（1）利用兩個向量的數量積公式，兩角和的正弦公式，求出函數f（x）=sin（2x﹣ 
），從而得到f（x）的最小正周期；（2）由x的范圍求得相應的范圍，再由正弦曲線y=sinx在[ ， ]上的圖象進一步求得f（x）在[0， ]上的最大值和最小值．
名師導航單元期末沖刺100分系列答案科目：高中數學 來源： 題型：
【題目】某中學團委組織了“弘揚奧運精神，愛我中華”的知識競賽，從參加考試的學生中抽出60名學生，將其成績（均為整數）分成六段[40，50），[50，60），…，[90，100〕后畫出如圖所示的頻率分布直方圖．觀察圖形給出的信息，回答下列問題：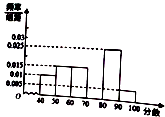 
（1）求第四小組的頻率，并補全這個頻率分布直方圖；
（2）估計這次考試的及格率（60分及以上為及格）和平均分．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】若
能構成映射，下列說法正確的有 （ ）
（1）A中的任一元素在B中必須有像且唯一；
（2）A中的多個元素可以在B中有相同的像；
（3）B中的多個元素可以在A中有相同的原像；
（4）像的集合就是集合B.
A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】為落實《課標》所倡導的課程理念，切實提高學生的綜合素質，某校高二年級開設“趣味數學”、“趣味物理”、“趣味化學”3門任意選修課程，供年級300位文科生自由選擇2門（不可多選或少選），選課情況如下表：
（Ⅰ）為了解學生選課情況，現采用分層抽樣方法抽取了三科作業共50本，統計發現“趣味物理”有18本，試根據這一數據估計
， 
的值；
（Ⅱ）為方便開課，學校要求
， 
，計算
的概率.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
．
（Ⅰ）當
時，求函數
的極小值；
（Ⅱ）設定義在
上的函數
在點
處的切線方程為
：
，當
時，若
在內恒成立，則稱
為函數
的“轉點”．當
時，試問函數是否存在“轉點”？若存在，求出轉點的橫坐標；若不存在，請說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在三棱柱ABC﹣A1B1C1中，側棱AA1⊥底面ABC，AC=3，BC=4，AB=5，AA1=4，點D是AB的中點．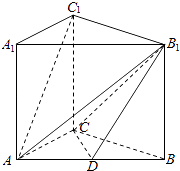 
（1）求證：AC1∥平面CDB1
（2）求證：AC⊥BC1
（3）求直線AB1與平面BB1C1C所成的角的正切值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知向量
，函數
，且
圖象上一個最高點為
與
最近的一個最低點的坐標為
.
(Ⅰ)求函數的解析式；
(Ⅱ)設
為常數，判斷方程
在區間
上的解的個數；
（Ⅲ）在銳角
中，若
，求
的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設偶函數f（x）的定義域為[﹣4，0）∪（0，4]，若當x∈（0，4]時，f（x）=log2x，
（1）求出函數在定義域[﹣4，0）∪（0，4]的解析式；
（2）求不等式xf（x）＜0得解集．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com