
【題目】已知橢圓![]() 的右焦點為
的右焦點為![]() ,點
,點![]() 在橢圓
在橢圓![]() 上,點
上,點![]() 在圓
在圓![]() 上,且圓
上,且圓![]() 上的所有點均在橢圓
上的所有點均在橢圓![]() 外,若
外,若![]() 的最小值為
的最小值為![]() ,且橢圓
,且橢圓![]() 的長軸長恰與圓
的長軸長恰與圓![]() 的直徑長相等,則下列說法正確的是( )
的直徑長相等,則下列說法正確的是( )
A.橢圓![]() 的焦距為
的焦距為![]() B.橢圓
B.橢圓![]() 的短軸長為
的短軸長為![]()
C.![]() 的最小值為
的最小值為![]() D.過點
D.過點![]() 的圓
的圓![]() 的切線斜率為
的切線斜率為![]()
【答案】AD
【解析】
由題意可求得![]() 的值,再由圓的幾何性質結合橢圓的定義以及已知條件可求得
的值,再由圓的幾何性質結合橢圓的定義以及已知條件可求得![]() 的值,進而可判斷出A、B選項的正誤;利用圓的幾何性質可判斷C選項的正誤;設出切線方程,利用圓心到切線的距離等于半徑可求得切線的斜率,可判斷D選項的正誤.綜合可得出結論.
的值,進而可判斷出A、B選項的正誤;利用圓的幾何性質可判斷C選項的正誤;設出切線方程,利用圓心到切線的距離等于半徑可求得切線的斜率,可判斷D選項的正誤.綜合可得出結論.
圓![]() 的圓心為
的圓心為![]() ,半徑長為
,半徑長為![]() ,
,
由于橢圓![]() 的長軸長恰與圓
的長軸長恰與圓![]() 的直徑長相等,則
的直徑長相等,則![]() ,可得
,可得![]() ,
,
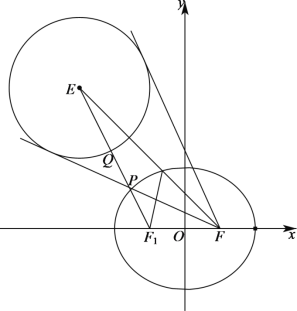
設橢圓的左焦點為點![]() ,由橢圓的定義可得
,由橢圓的定義可得![]() ,
,![]() ,
,
所以,![]() ,
,
當且僅當![]() 、
、![]() 、
、![]() 、
、![]() 四點共線,且當
四點共線,且當![]() 、
、![]() 分別為線段
分別為線段![]() 與橢圓
與橢圓![]() 、圓
、圓![]() 的交點時,等號成立,
的交點時,等號成立,
則![]() ,
,![]() ,解得
,解得![]() ,
,
所以,橢圓![]() 的焦距為
的焦距為![]() ,A選項正確;
,A選項正確;
橢圓![]() 的短軸長為
的短軸長為![]() ,B選項錯誤;
,B選項錯誤;
![]() ,
,
當且僅當![]() 、
、![]() 、
、![]() 、
、![]() 四點共線,且當
四點共線,且當![]() 、
、![]() 分別為線段
分別為線段![]() 與橢圓
與橢圓![]() 、圓
、圓![]() 的交點時,等號成立,C選項錯誤;
的交點時,等號成立,C選項錯誤;
若所求切線的斜率不存在,則直線方程為![]() ,圓心
,圓心![]() 到該直線的距離為
到該直線的距離為![]() ,則直線
,則直線![]() 與圓
與圓![]() 相離,不合乎題意;
相離,不合乎題意;
若所求切線的斜率存在,可設切線的方程為![]() ,即
,即![]() ,
,
由題意可得![]() ,整理得
,整理得![]() ,解得
,解得![]() .
.
D選項正確.
故選:AD.


 每日10分鐘口算心算速算天天練系列答案
每日10分鐘口算心算速算天天練系列答案科目:高中數學 來源: 題型:
【題目】在①![]() ,②
,②![]() ,③
,③![]() 這三個條件中任選一個,補充在下面問題中,若問題中的三角形存在,求
這三個條件中任選一個,補充在下面問題中,若問題中的三角形存在,求![]() 的值;若問題中的三角形不存在,說明理由.
的值;若問題中的三角形不存在,說明理由.
問題:是否存在![]() ,它的內角
,它的內角![]() 的對邊分別為
的對邊分別為![]() ,且
,且![]() ,
,![]() ,________?
,________?
注:如果選擇多個條件分別解答,按第一個解答計分.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為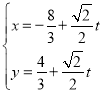 (
(![]() 為參數).以坐標原點
為參數).以坐標原點![]() 為極點,
為極點,![]() 軸的正半軸為極軸建立極坐標系,曲線
軸的正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() ,其中
,其中![]() .
.
(Ⅰ)寫出直線![]() 的普通方程和曲線
的普通方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(Ⅱ)在平面直角坐標系![]() 中,設直線
中,設直線![]() 與曲線
與曲線![]() 相交于
相交于![]() ,
,![]() 兩點.若點
兩點.若點![]() 恰為線段
恰為線段![]() 的三等分點,求
的三等分點,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】洛書,古稱龜書,是陰陽五行術數之源,被世界公認為組合數學的鼻祖,它是中華民族對人類的偉大貢獻之一.在古代傳說中有神龜出于洛水,其甲殼上有圖1:“以五居中,五方白圈皆陽數,四隅黑點為陰數”,這就是最早的三階幻方,按照上述說法,將1到9這九個數字,填在如圖2所示的九宮格里,九宮格的中間填5,四個角填偶數,其余位置填奇數.則每一橫行、每一豎列以及兩條對角線上3個數字的和都等于15的概率是( )
圖1 圖2
圖2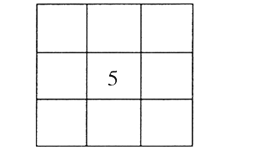
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com