
在ΔABC中,頂點A,B, C所對三邊分別是a,b,c已知B(-1, 0), C(1, 0),且b,a, c成等差數列.
(I )求頂點A的軌跡方程;
(II) 設頂點A的軌跡與直線y=kx+m相交于不同的兩點M、N,如果存在過點P(0,-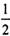 )的直線l,使得點M、N關于l對稱,求實數m的取值范圍
)的直線l,使得點M、N關于l對稱,求實數m的取值范圍
(1)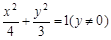 (2)當k=0時,m的取值范圍為
(2)當k=0時,m的取值范圍為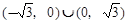 ;
;
當k≠0時,m的取值范圍為(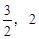 ).
).
【解析】(I ) 且b,a, c成等差數列結合橢圓的定義求得軌跡方程;(II)將y=kx+m與橢圓方程聯立,判別式大于0,根據點關于直線對稱,得k、m的關系
解:(I)由題知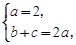 得b+c=4,即|AC|+|AB|=4(定值).
得b+c=4,即|AC|+|AB|=4(定值).
由橢圓定義知,頂點A的軌跡是以B、C為焦點的橢圓(除去左右頂點),
且其長半軸長為2,半焦距為1,于是短半軸長為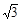 .
.
∴
頂點A的軌跡方程為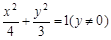 .………………………………4分
.………………………………4分
(II)由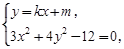
消去y整理得(3+4k2)x2+8kmx+4(m2-3)=0.∴ Δ=(8km)2-4(3+4k2)×4(m2-3)>0,
整理得:4k2>m2-3.①令M(x1,y1),N(x2,y2),則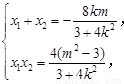
設MN的中點P(x0,y0),則
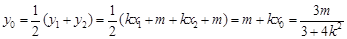 ,…………………7分
,…………………7分
i)當k=0時,由題知,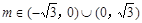 .……………………………8分
.……………………………8分
ii)當k≠0時,直線l方程為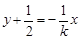 ,由P(x0,y0)在直線l上,得
,由P(x0,y0)在直線l上,得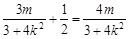 ,得2m=3+4k2.②把②式代入①中可得2m-3>m2-3,解得0<m<2.又由②得2m-3=4k2>0,解得
,得2m=3+4k2.②把②式代入①中可得2m-3>m2-3,解得0<m<2.又由②得2m-3=4k2>0,解得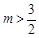 .∴
.∴ 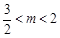 .驗證:當(-2,0)在y=kx+m上時,得m=2k代入②得4k2-4k+3=0,k無解.即y=kx+m不會過橢圓左頂點.同理可驗證y=kx+m不過右頂點.∴ m的取值范圍為(
.驗證:當(-2,0)在y=kx+m上時,得m=2k代入②得4k2-4k+3=0,k無解.即y=kx+m不會過橢圓左頂點.同理可驗證y=kx+m不過右頂點.∴ m的取值范圍為(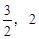 ).………11分
).………11分
綜上,當k=0時,m的取值范圍為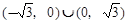 ;當k≠0時,m的取值范圍為(
;當k≠0時,m的取值范圍為(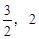 ).
).


科目:高中數學 來源: 題型:
| CM |
| CN |
| CM |
| CN |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 1 | 2 |
查看答案和解析>>
科目:高中數學 來源:2011-2012學年河南鄭州高三第一次質量預測理數學試卷(解析版) 題型:解答題
在△ABC中,頂點A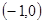 ,B
,B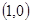 ,動點D,E滿足:①
,動點D,E滿足:①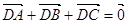 ;②
;②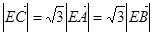 ,③
,③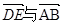 共線.
共線.
(Ⅰ)求△ABC頂點C的軌跡方程;
(Ⅱ)是否存在圓心在原點的圓,只要該圓的切線與頂點C的軌跡有兩個不同交點M,N,就一定有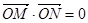 ,若存在,求該圓的方程;若不存在,請說明理由.
,若存在,求該圓的方程;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源:2011-2012學年河南鄭州高三第一次質量預測文科數學試卷(解析版) 題型:解答題
在△ABC中,頂點A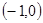 ,B
,B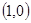 ,動點D,E滿足:①
,動點D,E滿足:①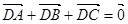 ;②
;②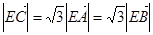 ,③
,③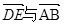 共線.
共線.
(Ⅰ)求△ABC頂點C的軌跡方程;
(Ⅱ)若斜率為1直線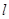 與動點C的軌跡交與M,N兩點,且
與動點C的軌跡交與M,N兩點,且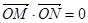 ,求直線
,求直線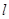 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源:2011-2012學年河南省鎮平一高高三下學期第四次周考文科數學試卷 題型:解答題
.(本小題滿分12分)
在△ABC中,頂點A(-1,0),B(1,0),動點D,E滿足:
①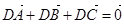 ;②|
;②|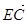 |=
|=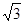 |
|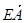 |=
|=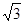 |
|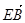 |③
|③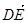 與
與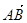 共線.
共線.
(Ⅰ)求△ABC頂點C的軌跡方程;
(Ⅱ)
若斜率為1直線l與動點C的軌跡交于M,N兩點,且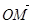 ·
·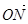 =0,求直線l的方程.
=0,求直線l的方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com