
【題目】已知函數![]() .
.
(1)若![]() ,求曲線
,求曲線![]() 在點
在點![]() 處的切線方程;
處的切線方程;
(2)求證:函數![]() 有且只有一個零點.
有且只有一個零點.
【答案】(1)![]() ;(2)詳見解析.
;(2)詳見解析.
【解析】
(1)對函數進行求導,求出切線的斜率和切點坐標,即可得答案;
(2)函數的定義域為![]() ,要使函數
,要使函數![]() 有且只有一個零點,只需方程
有且只有一個零點,只需方程![]() 有且只有一個根,即只需關于x的方程
有且只有一個根,即只需關于x的方程![]() 在
在![]() 上有且只有一個解,利用導數可得函數
上有且只有一個解,利用導數可得函數![]() 在
在![]() 單調遞增,再利用零點存在定理,即可得答案;
單調遞增,再利用零點存在定理,即可得答案;
(1)當![]() 時,函數
時,函數![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
所以函數![]() 在點
在點![]() 處的切線方程是
處的切線方程是![]() .
.
(2)函數的定義域為![]() ,
,
要使函數![]() 有且只有一個零點,只需方程
有且只有一個零點,只需方程![]() 有且只有一個根,
有且只有一個根,
即只需關于x的方程![]() 在
在![]() 上有且只有一個解.
上有且只有一個解.
設函數![]() ,
,
則![]() ,
,
令![]() ,
,
則/span>![]() ,
,
由![]() ,得
,得![]() .
.
x |
|
|
|
|
|
|
|
| 單調遞減 | 極小值 | 單調遞增 |
由于![]() ,
,
所以![]() ,
,
所以![]() 在
在![]() 上單調遞增,
上單調遞增,
又![]() ,
,![]() ,
,
①當![]() 時,
時, ![]() ,函數
,函數![]() 在
在![]() 有且只有一個零點,
有且只有一個零點,
②當![]() 時,由于
時,由于![]() ,所以存在唯一零點.
,所以存在唯一零點.
綜上所述,對任意的![]() 函數
函數![]() 有且只有一個零點.
有且只有一個零點.


 世紀百通期末金卷系列答案
世紀百通期末金卷系列答案科目:高中數學 來源: 題型:
【題目】金秋九月,丹桂飄香,某高校迎來了一大批優秀的學生,新生接待其實也是和社會溝通的一個平臺.校團委、學生會從在校學生中隨機抽取了160名學生,對是否愿意投入到新生接待工作進行了問卷調查,統計數據如下:
愿意 | 不愿意 | |
男生 | 60 | 20 |
女生 | 40 | 40 |
(1)通過估算,試判斷男、女哪種性別的學生愿意投入到新生接待工作的概率更大.
(2)能否有99%的把握認為,愿意參加新生接待工作與性別有關?
附: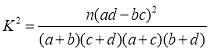 ,其中
,其中![]() .
.
| 0.05 | 0.01 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,橢圓![]() 的左、右頂點分別為
的左、右頂點分別為![]() ,
,![]() ,上、下頂點分別為
,上、下頂點分別為![]() ,
,![]() ,且
,且![]() ,
,![]() 為等邊三角形,過點
為等邊三角形,過點![]() 的直線與橢圓
的直線與橢圓![]() 在
在![]() 軸右側的部分交于
軸右側的部分交于![]() 、
、![]() 兩點.
兩點.

(1)求橢圓![]() 的標準方程;
的標準方程;
(2)求四邊形![]() 面積的取值范圍.
面積的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,平面
中,平面![]() 平面ABCD,
平面ABCD,![]() ,
,![]() ,底面ABCD是邊長為2的菱形,點E,F分別為棱DC,BC的中點,點G是棱SC靠近點C的四等分點.
,底面ABCD是邊長為2的菱形,點E,F分別為棱DC,BC的中點,點G是棱SC靠近點C的四等分點.
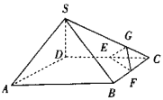
求證:(1)直線![]() 平面EFG;
平面EFG;
(2)直線![]() 平面SDB.
平面SDB.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
:![]() 的離心率
的離心率![]() ,左、右焦點分別為
,左、右焦點分別為![]() 、
、![]() ,拋物線
,拋物線![]() 的焦點
的焦點![]() 恰好是該橢圓的一個頂點.
恰好是該橢圓的一個頂點.
(1)求橢圓![]() 的方程;
的方程;
(2)已知直線![]() :
:![]() 與圓
與圓![]() :
:![]() 相切,且直線
相切,且直線![]() 與橢圓相交于
與橢圓相交于![]() 、
、![]() 兩點,求
兩點,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知拋物線![]() 的焦點為
的焦點為![]() .
.
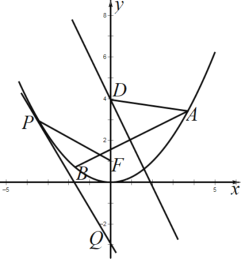
![]() 若點
若點![]() 為拋物線上異于原點的任一點,過點
為拋物線上異于原點的任一點,過點![]() 作拋物線的切線交
作拋物線的切線交![]() 軸于點
軸于點![]() ,證明:
,證明:![]() .
.
![]()
![]() ,
,![]() 是拋物線上兩點,線段
是拋物線上兩點,線段![]() 的垂直平分線交
的垂直平分線交![]() 軸于點
軸于點![]() (
(![]() 不與
不與![]() 軸平行),且
軸平行),且![]() .過
.過![]() 軸上一點
軸上一點![]() 作直線
作直線![]() 軸,且
軸,且![]() 被以
被以![]() 為直徑的圓截得的弦長為定值,求
為直徑的圓截得的弦長為定值,求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在四棱錐![]() 的底面
的底面![]() 中,
中,![]() ∥
∥![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,![]() 是
是![]() 的中點,且
的中點,且![]()
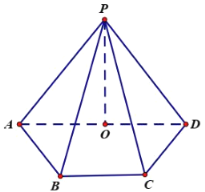
(1)求證:![]() ∥平面
∥平面![]() ;
;
(2)求二面角![]() 的余弦值;
的余弦值;
(3)在線段![]() 內是否存在點
內是否存在點![]() ,使得
,使得![]() ?若存在指出點
?若存在指出點![]() 的位置,若不存在,請說明理由.
的位置,若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com