
���}Ŀ����֪����(sh��)![]() .
.
��1����(d��ng)![]() �r(sh��)����(sh��)
�r(sh��)����(sh��)![]() �ĘOֵ��
�ĘOֵ��
��2��������(sh��)![]() �Ѓɂ�(g��)���c(di��n)
�Ѓɂ�(g��)���c(di��n)![]() ����
����![]() ��ȡֵ���������C��
��ȡֵ���������C��![]() .
.
���𰸡���1����(d��ng)![]() �r(sh��)��
�r(sh��)�� ![]() ��
��![]() ̎ȡ�õĘO��ֵ
̎ȡ�õĘO��ֵ![]() ������(sh��)
������(sh��)![]() �o(w��)�OСֵ. ��2��
�o(w��)�OСֵ. ��2��![]() �C��Ҋ(ji��n)����
�C��Ҋ(ji��n)����
��������ԇ�}��������1�����![]() ����
����![]() ���
���![]() �ķ������ɵú���(sh��)
�ķ������ɵú���(sh��)![]() ���^(q��)�g����
���^(q��)�g����![]() ���
���![]() �ķ������ɵú���(sh��)
�ķ������ɵú���(sh��)![]() �Ĝp�^(q��)�g���Ķ��ɵú���(sh��)
�Ĝp�^(q��)�g���Ķ��ɵú���(sh��)![]() �ĘOֵ����2����(du��)
�ĘOֵ����2����(du��)![]() �M(j��n)��ӑՓ��
�M(j��n)��ӑՓ�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��ᘌ�(du��)�����ķN��r���քe���Ì�(d��o)��(sh��)�о�����(sh��)�Ć��{(di��o)�������Æ��{(di��o)��ӑՓ����(sh��)
��ᘌ�(du��)�����ķN��r���քe���Ì�(d��o)��(sh��)�о�����(sh��)�Ć��{(di��o)�������Æ��{(di��o)��ӑՓ����(sh��)![]() �Ѓɂ�(g��)���c(di��n)��r���ų����ǃɂ�(g��)���c(di��n)����r���ɵ�
�Ѓɂ�(g��)���c(di��n)��r���ų����ǃɂ�(g��)���c(di��n)����r���ɵ�![]() �Ѓɂ�(g��)���c(di��n)�r(sh��)��
�Ѓɂ�(g��)���c(di��n)�r(sh��)�� ![]() ��ȡֵ������
��ȡֵ������![]() ���ɣ�1��֪
���ɣ�1��֪![]() ��
��![]() ���{(di��o)�f�p����ֻ���C��
���{(di��o)�f�p����ֻ���C��![]() ��������
��������![]() ��ֻ�����Ì�(d��o)��(sh��)�C��
��ֻ�����Ì�(d��o)��(sh��)�C��![]() ����.
����.
ԇ�}��������1����![]() ��
��![]() ��
��
��(d��ng)![]() �r(sh��)��
�r(sh��)�� ![]() ����
����![]() ����
����![]()
![]() ��
��
�ʮ�(d��ng)![]() �r(sh��)��
�r(sh��)�� ![]() ��
��![]() ̎ȡ�õĘO��ֵ
̎ȡ�õĘO��ֵ![]() ������(sh��)
������(sh��)![]() �o(w��)�OСֵ.
�o(w��)�OСֵ.
��2����(d��ng)![]() �r(sh��)���ɣ�1��֪
�r(sh��)���ɣ�1��֪![]() ��
��![]() ̎ȡ�ØO��ֵ
̎ȡ�ØO��ֵ![]() ���Ү�(d��ng)
���Ү�(d��ng)![]() څ����
څ����![]() �r(sh��)��
�r(sh��)�� ![]() څ����ؓ(f��)�o(w��)�F����
څ����ؓ(f��)�o(w��)�F����![]() �Ѓɂ�(g��)���c(di��n)���t
�Ѓɂ�(g��)���c(di��n)���t![]() �����
�����![]() .
.
��(d��ng)![]() �r(sh��)����
�r(sh��)����![]() ����
����![]() ����
����![]() ���t
���t![]() ��
��![]() ̎ȡ�ØO��ֵ����
̎ȡ�ØO��ֵ����![]() ̎ȡ�ØOСֵ������
̎ȡ�ØOСֵ������![]() ���t
���t![]() �H��һ��(g��)���c(di��n).
�H��һ��(g��)���c(di��n).
��(d��ng)![]() �r(sh��)��
�r(sh��)�� ![]() ���t
���t![]() �H��һ��(g��)���c(di��n).
�H��һ��(g��)���c(di��n).
��(d��ng)![]() �r(sh��)����
�r(sh��)����![]() ����
����![]() ����
����![]() ���t
���t![]() ��
��![]() ̎ȡ�ØOСֵ����
̎ȡ�ØOСֵ����![]() ̎ȡ�ØO��ֵ������
̎ȡ�ØO��ֵ������![]() ���t
���t![]() �H��һ��(g��)���c(di��n).
�H��һ��(g��)���c(di��n).
�C�ϣ� ![]() �Ѓɂ�(g��)���c(di��n)�r(sh��)��
�Ѓɂ�(g��)���c(di��n)�r(sh��)�� ![]() ��ȡֵ������
��ȡֵ������![]() .
.
�����c(di��n)�քe�څ^(q��)�g![]() ��
��![]() ��(n��i)�������O(sh��)
��(n��i)�������O(sh��)![]() .
.
���C![]() �����C��
�����C��![]() ��
��
���ɣ�1��֪![]() ��
��![]() ���{(di��o)�f�p����ֻ���C��
���{(di��o)�f�p����ֻ���C��![]() ����.
����.
![]() ��
��
��![]() ��
��
����![]() ��
��
��![]() ���t
���t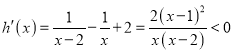 ��
��
�t![]() ��
��![]() �φ��{(di��o)�f�p������
�φ��{(di��o)�f�p������![]() ����
����![]() ��
��
����![]() .
.



| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����D����֪�������_(t��i)![]() �У�
��![]() ��
��![]() ��
��![]() .
.
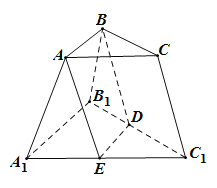
��1�����C��![]() ��
��
��2���^(gu��)![]() ��ƽ��
��ƽ��![]() �քe��
�քe��![]() ��
��![]() ���c(di��n)
���c(di��n)![]() ��
��![]() ���ҷָ������_(t��i)
���ҷָ������_(t��i)![]() ���Ãɲ��֎��w���w�e�Ȟ�
���Ãɲ��֎��w���w�e�Ȟ�![]() �����w
�����w![]() ����������
����������![]() ���L(zh��ng).
���L(zh��ng).
��ʾ���_(t��i)�w���w�e��ʽ![]() ��
��![]() ��
��![]() �քe�����_(t��i)���ϡ��µ�����e��
�քe�����_(t��i)���ϡ��µ�����e��![]() �����_(t��i)�ĸߣ�.
�����_(t��i)�ĸߣ�.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪����![]() ����
����![]() �c
�c![]() �ĊA�Ǟ�
�ĊA�Ǟ�![]() ���tֱ��
���tֱ��![]() �c�A
�c�A![]() ��λ���P(gu��n)ϵ�ǣ� ��
��λ���P(gu��n)ϵ�ǣ� ��
A.�ཻ�����^(gu��)�A��B.�ཻ���^(gu��)�A��C.����D.���x
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ���O(sh��)�E�A![]() ���x���ʞ�
���x���ʞ�![]() �����ҽ��c(di��n)�քe��
�����ҽ��c(di��n)�քe��![]()
![]() ���c(di��n)D�ڙE�AC�ϣ�
���c(di��n)D�ڙE�AC�ϣ�![]() �����L(zh��ng)��
�����L(zh��ng)��![]() .
.
��1����E�AC�Ę�(bi��o)��(zh��n)���̣�
��2���^(gu��)�A![]() ������һ�c(di��n)P���AE���о�l����l�c�E�AC����A��B���c(di��n)��O������(bi��o)ԭ�c(di��n)�����C��
������һ�c(di��n)P���AE���о�l����l�c�E�AC����A��B���c(di��n)��O������(bi��o)ԭ�c(di��n)�����C��![]() �鶨ֵ.
�鶨ֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪�E�A![]()
![]() ���x���ʞ�
���x���ʞ�![]() ������ԭ�c(di��n)O��A�ģ��E�AC���L(zh��ng)���S�L(zh��ng)��돽�ĈA�cֱ��
������ԭ�c(di��n)O��A�ģ��E�AC���L(zh��ng)���S�L(zh��ng)��돽�ĈA�cֱ��![]() ���У�
����
��1����E�A�Ę�(bi��o)��(zh��n)���̣�
��2����֪?ji��ng)�ֱ��l�^(gu��)�ҽ��c(di��n)F�����c�E�AC����A��B���c(di��n)����֪Q�c(di��n)����(bi��o)��![]() ����
����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪![]() �ǙE�A
�ǙE�A![]() �c���タ
�c���タ![]() ��һ��(g��)�����c(di��n)���ҙE�A�c���タ����һ��(g��)��ͬ�Ľ��c(di��n)
��һ��(g��)�����c(di��n)���ҙE�A�c���タ����һ��(g��)��ͬ�Ľ��c(di��n)![]() ��
��
��1����E�A![]() �����タ
�����タ![]() �ķ��̣�
�ķ��̣�
��2���O(sh��)�^(gu��)![]() �һ��ഹֱ�ăɄ�(d��ng)ֱ��
�һ��ഹֱ�ăɄ�(d��ng)ֱ��![]() ��
��![]() �c�E�A
�c�E�A![]() ����
����![]() ���c(di��n)��
���c(di��n)��![]() �c���タ
�c���タ![]() ����
����![]() ���c(di��n)������߅��
���c(di��n)������߅��![]() ��e����Сֵ
��e����Сֵ
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]() ������
������![]() ��
��
��1����(sh��)![]() ���{(di��o)�^(q��)�g��
���{(di��o)�^(q��)�g��
��2��������(sh��)![]() ���ڃɂ�(g��)�Oֵ�c(di��n)
���ڃɂ�(g��)�Oֵ�c(di��n)![]() ��
��![]() ����
����![]() ���C����
���C����![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ���O(sh��)����(sh��)![]() ��
��![]() .
.
��1���Дຯ��(sh��)��![]() ��
��![]() �Ć��{(di��o)�ԣ�
�Ć��{(di��o)�ԣ�
��2����(du��)�څ^(q��)�g![]() �ϵ����ⲻ��Ȍ�(sh��)��(sh��)
�ϵ����ⲻ��Ȍ�(sh��)��(sh��)![]() ��
��![]() ������
������![]() ��������(sh��)��(sh��)
��������(sh��)��(sh��)![]() ��ȡֵ����.
��ȡֵ����.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]() ��
��
��1���Дຯ��(sh��)![]() ����ż�ԣ����f(shu��)�����ɣ�
����ż�ԣ����f(shu��)�����ɣ�
��2����֪����ʽ![]() ��
��![]() �Ϻ��������(sh��)��(sh��)
�Ϻ��������(sh��)��(sh��)![]() �����ֵ��
�����ֵ��
��3����(d��ng)![]() �r(sh��)����(sh��)
�r(sh��)����(sh��)![]() �����c(di��n)��(g��)��(sh��)��
�����c(di��n)��(g��)��(sh��)��
�鿴�𰸺ͽ���>>
��(gu��)�H�W(xu��)У��(y��u)�x - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)��(zhu��n)�^(q��) | ����p�_�e��(b��o)��(zhu��n)�^(q��) | ��vʷ̓�o(w��)���x�к���Ϣ�e��(b��o)��(zhu��n)�^(q��) | �����֙�(qu��n)�e��(b��o)��(zhu��n)�^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com