
(本小題滿分13分)已知函數 .
.
(Ⅰ)當 時,求函數
時,求函數 的單調增區間;
的單調增區間;
(Ⅱ)求函數 在區間
在區間 上的最小值.
上的最小值.
(Ⅰ) 和
和 ;(Ⅱ)
;(Ⅱ)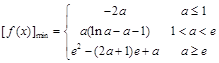
解析試題分析:(Ⅰ)利用導數,列表分析即可確定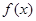 的單調增區間;(Ⅱ)
的單調增區間;(Ⅱ)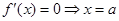 或
或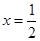 ,所以分成
,所以分成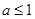 、
、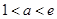 、
、 三種情況,利用導數,列表分析每一種情況下
三種情況,利用導數,列表分析每一種情況下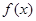 的最小值即可.
的最小值即可.
試題解析:(Ⅰ)當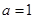 時,
時,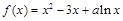 ,定義域為
,定義域為 .
.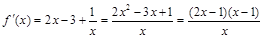 .
.
令 ,得
,得 或
或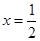 . 3分
. 3分
列表如下
所以函數



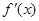
+ - + 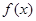
↗ ↘ ↗ 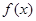 的單調增區間為
的單調增區間為 和
和 . 6分
. 6分
(Ⅱ)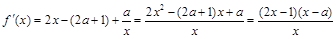 .
.
令 ,得
,得 或
或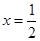 . ^ 7分
. ^ 7分
當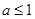 時,不論
時,不論 還是
還是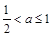 ,在區間
,在區間 上,
上, 均為增函數。
均為增函數。
所以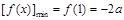 ; 8分
; 8分
當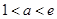 時,
時,