
【題目】在一個特定時段內,以點E為中心的7n mile以內海域被設為警戒水域.點E正北55n mile處有一個雷達觀測站A,某時刻測得一艘勻速直線行駛的船只位于點A北偏東45°且與點A相距40![]() n mile的位置B,經過40分鐘又測得該船已行駛到點A北偏東
n mile的位置B,經過40分鐘又測得該船已行駛到點A北偏東![]() (其中
(其中![]() ,
,![]() )且與點A相距10
)且與點A相距10![]() n mile的位置C.
n mile的位置C.
(I)求該船的行駛速度(單位:n mile /h);
(II)若該船不改變航行方向繼續行駛.判斷它是否會進入警戒水域,并說明理由.
【答案】(I)船的行駛速度為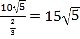 (海里/小時).(II)船會進入警戒水域.
(海里/小時).(II)船會進入警戒水域.
【解析】
試題(I)根據同角三角函數的基本關系式求出![]() ,然后利用余弦定理求出BC的值,從而可求出船的行駛速度.
,然后利用余弦定理求出BC的值,從而可求出船的行駛速度.
(II)判斷船是否會進入警戒水域,關鍵是看點E到直線l的距離與半徑7的關系,因而可求出直線l的方程,以及E點坐標,然后再根據點到直線的距離公式得到結論.
(I)如圖,AB=40![]() ,AC=10
,AC=10![]() ,
,![]()
由于![]() ,所以cos
,所以cos![]() =
=![]()
由余弦定理得BC=![]()
所以船的行駛速度為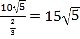 (海里/小時).
(海里/小時).
(II)解法一 如圖所示,以A為原點建立平面直角坐標系,
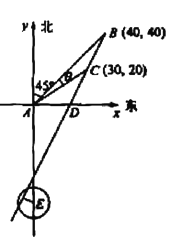
設點B、C的坐標分別是B(x1,y2), C(x1,y2),
BC與x軸的交點為D.
由題設有,x1=y1=![]() AB=40,
AB=40,
x2=ACcos![]() ,
,
y2=ACsin![]()
所以過點B、C的直線l的斜率k=![]() ,直線l的方程為y=2x-40.
,直線l的方程為y=2x-40.
又點E(0,-55)到直線l的距離d=![]()
所以船會進入警戒水域.
解法二: 如圖所示,設直線AE與BC的延長線相交于點Q.
在△ABC中,由余弦定理得,
![]() =
=![]() =
=![]() .
.
從而![]()
在![]() 中,由正弦定理得,AQ=
中,由正弦定理得,AQ=
由于AE=55>40=AQ,所以點Q位于點A和點E之間,且QE=AE-AQ=15.
過點E作EP![]() BC于點P,則EP為點E到直線BC的距離.
BC于點P,則EP為點E到直線BC的距離.![]()
在Rt![]() 中,PE=QE·sin
中,PE=QE·sin![]()
=![]() 所以船會進入警戒水域.
所以船會進入警戒水域.


科目:高中數學 來源: 題型:
【題目】如圖,在三棱錐![]() 中,
中,![]() 底面
底面![]() ,
,![]() .點
.點![]() 、
、![]() 、
、![]() 分別為棱
分別為棱![]() 、
、![]() 、
、![]() 的中點,
的中點,![]() 是線段
是線段![]() 的中點,
的中點,![]() ,
,![]() .
.
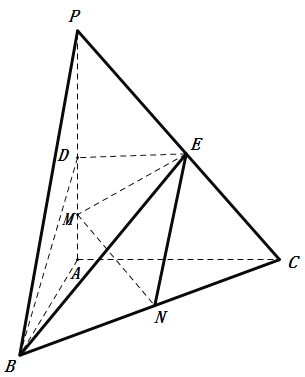
(1)求證:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的正弦值;
的正弦值;
(3)已知點![]() 在棱
在棱![]() 上,且直線
上,且直線![]() 與直線
與直線![]() 所成角的余弦值為
所成角的余弦值為![]() ,求線段
,求線段![]() 的長.
的長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點列![]() 為函數
為函數![]() 圖像上的點,點列
圖像上的點,點列![]() 順次為
順次為![]() 軸上的點,其中
軸上的點,其中![]() ,對任意
,對任意![]() ,點
,點![]() 構成以
構成以![]() 為頂點的等腰三角形.
為頂點的等腰三角形.
(1)證明:數列![]() 是等比數列;
是等比數列;
(2)若數列![]() 中任意連續三項能構成三角形的三邊,求
中任意連續三項能構成三角形的三邊,求![]() 的取值范圍;
的取值范圍;
(3)求證:對任意![]() ,
,![]() 是常數,并求數列
是常數,并求數列![]() 的通項公式.
的通項公式.
查看答案和解析>>
科目:高中數學 來源: 題型:
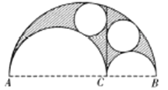
【題目】在一個半圓中有兩個互切的內切半圓,由三個半圓弧圍成曲邊三角形,作兩個內切半圓的公切線把曲邊三角形分隔成兩塊,阿基米德發現被分隔的這兩塊的內切圓是同樣大小的,由于其形狀很像皮匠用來切割皮料的刀子,他稱此為“皮匠刀定理”,如圖,若![]() ,則陰影部分與最大半圓的面積比為( )
,則陰影部分與最大半圓的面積比為( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
:![]() 的離心率
的離心率![]() ,且圓
,且圓![]() 過橢圓
過橢圓![]() 的上,下頂點.
的上,下頂點.
(1)求橢圓![]() 的方程.
的方程.
(2)若直線![]() 的斜率為
的斜率為![]() ,且直線
,且直線![]() 交橢圓
交橢圓![]() 于
于![]() 、
、![]() 兩點,點
兩點,點![]() 關于點的對稱點為
關于點的對稱點為![]() ,點
,點![]() 是橢圓
是橢圓![]() 上一點,判斷直線
上一點,判斷直線![]() 與
與![]() 的斜率之和是否為定值,如果是,請求出此定值:如果不是,請說明理.
的斜率之和是否為定值,如果是,請求出此定值:如果不是,請說明理.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知二次函數![]() 的值域為
的值域為![]() .
.
(1)判斷此函數的奇偶性,并說明理由;
(2)判斷此函數![]() 在的單調性,并用單調性的定義證明你的結論;
在的單調性,并用單調性的定義證明你的結論;
(3)求出![]() 在
在![]() 上的最小值
上的最小值![]() ,并求
,并求![]() 的值域.
的值域.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 為正方形,
為正方形,![]() 底面
底面![]() ,
,![]() ,
,![]() 為線段
為線段![]() 的中點,
的中點,![]() 為線段
為線段![]() 上的動點.
上的動點.
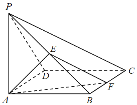
(1)求證:平面![]() 平面
平面![]() .
.
(2)試確定點![]() 的位置,使平面
的位置,使平面![]() 與平面
與平面![]() 所成的銳二面角為
所成的銳二面角為![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com