
【題目】已知函數(shù)![]() ,無(wú)窮數(shù)列
,無(wú)窮數(shù)列![]() 滿(mǎn)足
滿(mǎn)足![]() ,
, ![]()
(Ⅰ)若![]() ,求
,求![]() ,
, ![]() ,
, ![]() ;
;
(Ⅱ)若![]() ,且
,且![]() ,
, ![]() ,
, ![]() 成等比數(shù)列,求
成等比數(shù)列,求![]() 的值;
的值;
(Ⅲ)是否存在![]() ,使得
,使得![]() 成等差數(shù)列?若存在,求出所有這樣的
成等差數(shù)列?若存在,求出所有這樣的![]() ;若不存在,說(shuō)明理由.
;若不存在,說(shuō)明理由.
【答案】(Ⅰ) ![]() ;(Ⅱ)
;(Ⅱ) ![]() 或
或![]() .(Ⅲ)當(dāng)且僅當(dāng)
.(Ⅲ)當(dāng)且僅當(dāng)![]() 時(shí),
時(shí), ![]() ,構(gòu)成等差數(shù)列.
,構(gòu)成等差數(shù)列.
【解析】試題分析:
(Ⅰ)根據(jù)遞推關(guān)系求解即可.(Ⅱ)由條件得![]() ,
, ![]() ,分類(lèi)討論去掉絕對(duì)值,并根據(jù)
,分類(lèi)討論去掉絕對(duì)值,并根據(jù)![]() ,
, ![]() ,
, ![]() 成等比數(shù)列可求得
成等比數(shù)列可求得![]() 的值.(Ⅲ)由條件得
的值.(Ⅲ)由條件得![]() ,假設(shè)存在
,假設(shè)存在![]() 滿(mǎn)足條件,則
滿(mǎn)足條件,則![]() ,即
,即![]() ,經(jīng)分類(lèi)討論去掉絕對(duì)值可得當(dāng)且僅當(dāng)
,經(jīng)分類(lèi)討論去掉絕對(duì)值可得當(dāng)且僅當(dāng)![]() 時(shí),
時(shí), ![]() ,構(gòu)成等差數(shù)列.
,構(gòu)成等差數(shù)列.
試題解析:
(Ⅰ)![]() .
.
(Ⅱ)由題意得![]()
![]() .
.
當(dāng)![]() 時(shí),
時(shí), ![]() ,
,
∵![]() ,
, ![]() ,
, ![]() 成等比數(shù)列,
成等比數(shù)列,
∴![]() ,
,
解得![]() .
.
當(dāng)![]() 時(shí),
時(shí), ![]() ,
,
∵![]() ,
, ![]() ,
, ![]() 成等比數(shù)列
成等比數(shù)列
∴![]() ,
,
解得![]() (舍去).
(舍去).
綜上可得![]() 或
或![]() .
.
(Ⅲ)假設(shè)這樣的等差數(shù)列存在,那么![]() .
.
由![]() 得
得![]()
![]() .
.
以下分情況討論:
①當(dāng)![]() 時(shí),由
時(shí),由![]() 得
得![]() ,與
,與![]() 矛盾;
矛盾;
②當(dāng)![]() 時(shí),由
時(shí),由![]() 得
得![]() ,①
,①
從而![]() ,所以
,所以![]() 是一個(gè)等差數(shù)列;
是一個(gè)等差數(shù)列;
③當(dāng)![]() 時(shí),則公差
時(shí),則公差![]() ,
,
因此存在![]() 使得
使得![]() .
.
此時(shí)![]() ,與
,與![]() 矛盾.
矛盾.
綜合①②③可知,當(dāng)且僅當(dāng)![]() 時(shí),
時(shí), ![]() 構(gòu)成等差數(shù)列.
構(gòu)成等差數(shù)列.


 閱讀快車(chē)系列答案
閱讀快車(chē)系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖所示,已知![]() 是直角梯形,
是直角梯形, ![]() ,
, ![]() ,
, ![]() 平面
平面![]() .
.
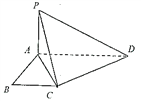
(1)證明: ![]() ;
;
(2)若![]() 是
是![]() 的中點(diǎn),證明:
的中點(diǎn),證明: ![]() 平面
平面![]() ;
;
(3)若![]() ,求三棱錐
,求三棱錐![]() 的體積.
的體積.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]() .
.
(1)求函數(shù)![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(2)若關(guān)于![]() 的不等式
的不等式![]() 恒成立,求整數(shù)
恒成立,求整數(shù)![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]() (m、n為常數(shù),e = 2.718 28…是自然對(duì)數(shù)的底數(shù)),曲線y = f (x)在點(diǎn)(1,f (1))處的切線方程是
(m、n為常數(shù),e = 2.718 28…是自然對(duì)數(shù)的底數(shù)),曲線y = f (x)在點(diǎn)(1,f (1))處的切線方程是![]() .
.
(Ⅰ)求m、n的值;
(Ⅱ)求f (x)的最大值;
(Ⅲ)設(shè)![]() (其中
(其中![]() 為f (x)的導(dǎo)函數(shù)),證明:對(duì)任意x > 0,都有
為f (x)的導(dǎo)函數(shù)),證明:對(duì)任意x > 0,都有![]() .
.
(注: ![]() )
)
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】下列說(shuō)法:
①將一組數(shù)據(jù)中的每個(gè)數(shù)據(jù)都加上或減去同一個(gè)常數(shù)后,方差恒不變;
②設(shè)有一個(gè)回歸方程![]() =3-5x,變量x增加一個(gè)單位時(shí),y平均增加5個(gè)單位;
=3-5x,變量x增加一個(gè)單位時(shí),y平均增加5個(gè)單位;
③線性回歸方程![]() =
=![]() x+
x+![]() 必過(guò)(
必過(guò)(![]() ,
,![]() );
);
④在一個(gè)2×2列聯(lián)表中,由計(jì)算得K2=13.079,則有99%以上的把握認(rèn)為這兩個(gè)變量間有關(guān)系.
其中錯(cuò)誤的個(gè)數(shù)是( )
本題可以參考獨(dú)立性檢驗(yàn)臨界值表:
P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
A. 0 B. 1
C. 2 D. 3
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]() 是偶函數(shù),
是偶函數(shù), ![]() 是
是![]() 上的奇函數(shù).
上的奇函數(shù).
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)若對(duì)![]() ,都有
,都有![]() 成立,求實(shí)數(shù)
成立,求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知點(diǎn)![]() 及圓
及圓![]() .
.
(1)設(shè)過(guò)點(diǎn)![]() 的直線
的直線![]() 與圓
與圓![]() 交于
交于![]() 兩點(diǎn),當(dāng)
兩點(diǎn),當(dāng)![]() 時(shí),求以線段
時(shí),求以線段![]() 為直徑的圓
為直徑的圓![]() 的方程;
的方程;
(2)設(shè)直線![]() 與圓
與圓![]() 交于
交于![]() 兩點(diǎn),是否存在實(shí)數(shù)
兩點(diǎn),是否存在實(shí)數(shù)![]() ,使得過(guò)點(diǎn)
,使得過(guò)點(diǎn)![]() 的直線
的直線![]() 垂直平分弦
垂直平分弦![]() ?若存在,求出實(shí)數(shù)
?若存在,求出實(shí)數(shù)![]() 的值;若不存在,請(qǐng)說(shuō)明理由.
的值;若不存在,請(qǐng)說(shuō)明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知橢圓![]()
![]() 的左、右焦點(diǎn)分別為
的左、右焦點(diǎn)分別為![]() ,
, ![]() ,直線
,直線![]() 交橢圓
交橢圓![]() 于
于![]() ,
, ![]() 兩點(diǎn),
兩點(diǎn), ![]() 的周長(zhǎng)為16,
的周長(zhǎng)為16, ![]() 的周長(zhǎng)為12.
的周長(zhǎng)為12.
(1)求橢圓![]() 的標(biāo)準(zhǔn)方程與離心率;
的標(biāo)準(zhǔn)方程與離心率;
(2)若直線![]() 與橢圓
與橢圓![]() 交于
交于![]() 兩點(diǎn),且
兩點(diǎn),且![]() 是線段
是線段![]() 的中點(diǎn),求直線
的中點(diǎn),求直線![]() 的一般方程.
的一般方程.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知長(zhǎng)方體![]() 中,
中, ![]() 為
為![]() 的中點(diǎn),如圖所示.
的中點(diǎn),如圖所示.
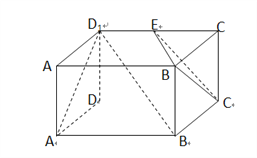
(1) 證明: ![]() 平面
平面![]() ;
;
(2) 求平面![]() 與平面
與平面![]() 所成銳二面角的大小的余弦值.
所成銳二面角的大小的余弦值.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com