
���}Ŀ����֪�c(di��n)![]() ���A
���A![]() .
.
��1���O(sh��)�^�c(di��n)![]() ��ֱ��
��ֱ��![]() �c�A
�c�A![]() ����
����![]() ���c(di��n)����(d��ng)
���c(di��n)����(d��ng)![]() �r(sh��)�����Ծ���
�r(sh��)�����Ծ���![]() ��ֱ���ĈA
��ֱ���ĈA![]() �ķ��̣�
�ķ��̣�
��2���O(sh��)ֱ��![]() �c�A
�c�A![]() ����
����![]() ���c(di��n)���Ƿ���ڌ�(sh��)��(sh��)
���c(di��n)���Ƿ���ڌ�(sh��)��(sh��)![]() ��ʹ���^�c(di��n)
��ʹ���^�c(di��n)![]() ��ֱ��
��ֱ��![]() ��ֱƽ����
��ֱƽ����![]() �������ڣ������(sh��)��(sh��)
�������ڣ������(sh��)��(sh��)![]() ��ֵ���������ڣ�Ո�f������.
��ֵ���������ڣ�Ո�f������.
���𰸡�(1) ![]() ��2�������ڌ�(sh��)��(sh��)
��2�������ڌ�(sh��)��(sh��)![]() ��ʹ���^�c(di��n)
��ʹ���^�c(di��n)![]() ��ֱ��
��ֱ��![]() ��ֱƽ����
��ֱƽ����![]()
��������ԇ�}��������1�������Ã��c(di��n)�g�ľ��x��ʽ����A��C��P�ľ��x���ٸ���(j��)���L|MN|��һ�뼰�돽�����ù��ɶ���������ľ�d���l(f��)�F(xi��n)|CP|�cd��ȣ����Եõ�P��MN�����c(di��n)��������MN��ֱ���ĈA�ĈA������(bi��o)����P������(bi��o)���돽��|MN|��һ�룬����(j��)�A�ĺͰ돽�����A�ķ��̼��ɣ���2������ֱ֪���ķ��̴��뵽�A�ķ�������ȥy�õ��P(gu��n)��x��һԪ���η��̣���?y��n)�ֱ���c�A�Ѓɂ�(g��)���c(di��n)�����Եõ�����0���г��P(gu��n)��a�IJ���ʽ���������ʽ�Ľ⼯���ɵõ�a��ȡֵ���������÷��C���C���C��������
ԇ�}������
�������ڈA![]() �ĈA��
�ĈA��![]() ���돽��
���돽��![]() ��
�� ![]() �������ľ�
�������ľ�![]() ��
��
����![]() ������
������![]() ��
��![]() �����c(di��n)��
�����c(di��n)��
��������A�ĈA������(bi��o)��![]() ���돽��
���돽��![]() ��
��
����![]() ��ֱ���ĈA
��ֱ���ĈA![]() �ķ��̞飺
�ķ��̞飺 ![]() ��
��
����ֱ��![]() ��
��![]() ����A
����A![]() �ķ��̣���ȥ
�ķ��̣���ȥ![]() �������ã�
�������ã�
![]() ��
��
����ֱ��![]() ���A
���A![]() ��
��![]() ��
�� ![]() ���c(di��n)��
���c(di��n)��
��![]() ����
����![]() �����
�����![]() ��
��
�t��(sh��)��(sh��)![]() ��ȡֵ������
��ȡֵ������![]() ��
��
�O(sh��)���ϗl���Č�(sh��)��(sh��)![]() ���ڣ�
���ڣ�
����![]() ��ֱƽ����
��ֱƽ����![]() ���ʈA��
���ʈA��![]() ����ֱ��
����ֱ��![]() �ϣ�
�ϣ�
����![]() ���
���![]() ������
������![]() ��
��
����![]() ��
��
�ʲ����ڌ�(sh��)��(sh��)![]() ��ʹ���^�c(di��n)
��ʹ���^�c(di��n)![]() ��ֱ��
��ֱ��![]() ��ֱƽ����
��ֱƽ����![]() ��
��



| �꼉 | �����n�� | �꼉 | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ���O(sh��)����(sh��) ![]() ��
��
���������� ![]() ���c(di��n)
���c(di��n) ![]() ̎���о����̣�
̎���о����̣�
������ ![]() ��
�� ![]() ���������(sh��)��(sh��)
���������(sh��)��(sh��) ![]() ��ȡֵ������
��ȡֵ������
����������(sh��) ![]() ��ֵ��ʹ����(sh��)
��ֵ��ʹ����(sh��) ![]() �څ^(q��)�g
�څ^(q��)�g ![]() �������c(di��n)��
�������c(di��n)��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����D����֪�����F![]() �У�����
�У�����![]() ��߅�L��1�������Σ���(c��)��
��߅�L��1�������Σ���(c��)��![]() ����
����![]() ����
����![]() ��
�� ![]() �ǂ�(c��)��
�ǂ�(c��)��![]() �ϵĄ�(d��ng)�c(di��n).
�ϵĄ�(d��ng)�c(di��n).
��1���������F![]() �ı���e��
�ı���e��
��2���Ƿ�����![]() �ϴ���һ�c(di��n)
�ϴ���һ�c(di��n)![]() ��ʹ��
��ʹ��![]() ƽ��
ƽ��![]() �������ڣ�ָ���c(di��n)
�������ڣ�ָ���c(di��n)![]() ��λ�ã����C�����������ڣ�Ո�f������.
��λ�ã����C�����������ڣ�Ո�f������.

�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ�������ڲ�����ij���(sh��)![]() ��ʹ�ú���(sh��)
��ʹ�ú���(sh��)![]() �����x���(n��i)����һ
�����x���(n��i)����һ![]() ����
����![]() ���t�Q����(sh��)
���t�Q����(sh��)![]() �����ں���(sh��)�����г���(sh��)
�����ں���(sh��)�����г���(sh��)![]() ���Ǻ���(sh��)��һ��(g��)����.
���Ǻ���(sh��)��һ��(g��)����.
��1���C���������ڲ�����ij���(sh��)![]() ʹ�ú���(sh��)
ʹ�ú���(sh��) ![]() �����x���(n��i)����һ
�����x���(n��i)����һ![]() ����
����![]() ���t�˺���(sh��)�����ں���(sh��).
���t�˺���(sh��)�����ں���(sh��).
��2�������x��![]() �ϵ��溯��(sh��)
�ϵ��溯��(sh��)![]() �M��
�M��![]() ��ԇ̽���˺���(sh��)�څ^(q��)�g
��ԇ̽���˺���(sh��)�څ^(q��)�g![]()
��(n��i)���c(di��n)�����ق�(g��)��(sh��).
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪��(f��)��(sh��)z=��m2+5m��6��+��m2��2m��15��i����i��̓��(sh��)��λ��m��R��
��1�����(f��)��(sh��)Z�ڏ�(f��)ƽ���(n��i)����(y��ng)���c(di��n)λ�ڵ�һ�������Ľ�ƽ�־��ϣ���(sh��)��(sh��)M��ֵ��
��2����(d��ng)��(sh��)��(sh��)m=��1�r(sh��)���� ![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ���������(sh��)f��x��=ax2+2x��3�څ^(q��)�g�����ޣ�4�����dž��{(di��o)�f���ģ��t��(sh��)��(sh��)a��ȡֵ�����ǣ� ��
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����D���������F![]() �У������������
�������������![]() ��
�� ![]() ����
����![]() ��ԓ�����F����ҕ�D�͂�(c��)ҕ�D�������L��6�ĵ���ֱ��������.
��ԓ�����F����ҕ�D�͂�(c��)ҕ�D�������L��6�ĵ���ֱ��������.

��1����������(y��ng)�ĸ�ҕ�D�������ԓ��ҕ�D����e��
��2�����C�� ![]() ��
��
��3���������F![]() ������ֱ��.
������ֱ��.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ��ij�W(xu��)У�����{(di��o)��ϲ�g�Z�ČW(xu��)���c�Ԅe���P(gu��n)ϵ���S�C(j��)�{(di��o)����һЩ�W(xu��)����r�����w��(sh��)��(j��)�����
�{(di��o)��y(t��ng)Ӌ(j��) | ��ϲ�g�Z�� | ϲ�g�Z�� |
�� | 13 | 10 |
Ů | 7 | 20 |
�����Д�ϲ�g�Z�ČW(xu��)���Ƿ��c�Ԅe���P(gu��n)ϵ������(j��)���еĔ�(sh��)��(j��)���õ�K2���^�yֵk= ![]() ��4.844����?y��n)�k��3.841������(j��)�±��еą�����(sh��)��(j��)��
��4.844����?y��n)�k��3.841������(j��)�±��еą�����(sh��)��(j��)��
P��K2��k0�� | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
�ж�ϲ�g�Z�ČW(xu��)���c�Ԅe���P(gu��n)ϵ����ô�@�N�Д���e(cu��)�Ŀ����Ԟ飨 ��
A.95%
B.50%
C.25%
D.5%
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ������(sh��)![]() �ĈD����D��ʾ�����˵õ�����(sh��)
�ĈD����D��ʾ�����˵õ�����(sh��)![]() �ĈD���Ѻ���(sh��)
�ĈD���Ѻ���(sh��)![]() �ĈD�� ��
�ĈD�� ��
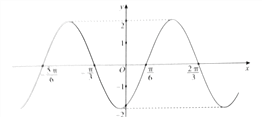
A. ÿ��(g��)�c(di��n)�ęM����(bi��o)�s�̵�ԭ����![]() ���v����(bi��o)��׃����������ƽ��
���v����(bi��o)��׃����������ƽ��![]() ��(g��)��λ
��(g��)��λ
B. ÿ��(g��)�c(di��n)�ęM����(bi��o)�s�̵�ԭ����2�����v����(bi��o)��׃����������ƽ��![]() ��(g��)��λ
��(g��)��λ
C. ������ƽ��![]() ��(g��)��λ���ٰ����ø��c(di��n)�ęM����(bi��o)���L��ԭ����2�����v����(bi��o)��׃��
��(g��)��λ���ٰ����ø��c(di��n)�ęM����(bi��o)���L��ԭ����2�����v����(bi��o)��׃��
D. ������ƽ��![]() ��(g��)��λ���ٰ����ø��c(di��n)�ęM����(bi��o)���L��ԭ����
��(g��)��λ���ٰ����ø��c(di��n)�ęM����(bi��o)���L��ԭ����![]() ���v����(bi��o)��׃��
���v����(bi��o)��׃��
�鿴�𰸺ͽ���>>
���H�W(xu��)У��(y��u)�x - ����(x��)���б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_ | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com