
【題目】在直三棱柱![]() 中,
中,![]() 為正三角形,點
為正三角形,點![]() 在棱
在棱![]() 上,且
上,且![]() ,點
,點![]() ,
,![]() 分別為棱
分別為棱![]() ,
,![]() 的中點.
的中點.
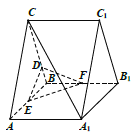
(1)證明:![]() 平面
平面![]() ;
;
(2)若![]() ,求直線
,求直線![]() 與平面
與平面![]() 所成的角的正弦值.
所成的角的正弦值.
【答案】(1)證明見解析;(2)![]() .
.
【解析】試題分析:(1)連接![]() ,
,![]() ,交于點
,交于點![]() ,
,![]() 交
交![]() 于點
于點![]() ,連接
,連接![]() ,易證
,易證![]() ,從而得證;(2)以點
,從而得證;(2)以點![]() 為坐標原點,分別以
為坐標原點,分別以![]() ,
,![]() ,
,![]() 的方向為
的方向為![]() 軸,
軸,![]() 軸,
軸,![]() 軸的正方向,建立空間直角坐標系,平面
軸的正方向,建立空間直角坐標系,平面![]() 的法向量為
的法向量為![]() ,
,![]() ,利用公式即可得到直線
,利用公式即可得到直線![]() 與平面
與平面![]() 所成的角的正弦值.
所成的角的正弦值.
試題解析:
(1)證明:如圖,連接![]() ,
,![]() ,交于點
,交于點![]() ,
,![]() 交
交![]() 于點
于點![]() ,連接
,連接![]() ,
,
因為![]() 為矩形,所以
為矩形,所以![]() 為線段
為線段![]() 的中點,
的中點,
因為點![]() ,
,![]() 分別為棱
分別為棱![]() ,
,![]() 的中點,
的中點,
所以點![]() 為線段
為線段![]() 的中點,所以
的中點,所以![]() ,
,
又因為![]() ,所以
,所以![]() ,
,
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ;
;
(2)由(1)知,![]() ,因為
,因為![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,
,
因為![]() 為正三角形,且點
為正三角形,且點![]() 為棱
為棱![]() 的中點,
的中點,
所以![]() ,
,
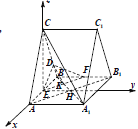
故以點![]() 為坐標原點,分別以
為坐標原點,分別以![]() ,
,![]() ,
,![]() 的方向為
的方向為![]() 軸,
軸,![]() 軸,
軸,![]() 軸的正方向,建立如圖所示的空間直角坐標系
軸的正方向,建立如圖所示的空間直角坐標系![]() ,設(shè)
,設(shè)![]() ,
,![]() ,
,
則![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,
因為![]() ,所以
,所以![]() ,
,
所以![]() ,解得
,解得![]() .
.
所以![]() ,
,![]() ,
,
設(shè)平面![]() 的法向量為
的法向量為![]() ,
,
則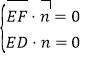 ,所以
,所以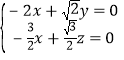 ,
,
取![]() ,則
,則![]() ,
,
又因為![]() ,設(shè)直線
,設(shè)直線![]() 與平面
與平面![]() 所成的角為
所成的角為![]() ,
,
所以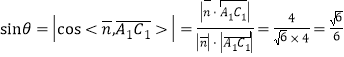 ,
,
所以直線![]() 與平面
與平面![]() 所成的角的正弦值為
所成的角的正弦值為![]() .
.


科目:高中數(shù)學 來源: 題型:
【題目】已知橢圓![]() :
:![]()
![]() 的一個焦點與拋物線
的一個焦點與拋物線![]() 的焦點重合,且過點
的焦點重合,且過點![]() .過點
.過點![]() 的直線
的直線![]() 交橢圓
交橢圓![]() 于
于![]() ,
, ![]() 兩點,
兩點, ![]() 為橢圓的左頂點.
為橢圓的左頂點.
(Ⅰ)求橢圓![]() 的標準方程;
的標準方程;
(Ⅱ)求![]() 面積的最大值,并求此時直線
面積的最大值,并求此時直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】【2018海南高三階段性測試(二模)】如圖,在直三棱柱![]() 中,
中, ![]() ,
, ![]() ,點
,點![]() 為
為![]() 的中點,點
的中點,點![]() 為
為![]() 上一動點.
上一動點.
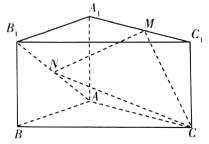
(I)是否存在一點![]() ,使得線段
,使得線段![]() 平面
平面![]() ?若存在,指出點
?若存在,指出點![]() 的位置,若不存在,請說明理由.
的位置,若不存在,請說明理由.
(II)若點![]() 為
為![]() 的中點且
的中點且![]() ,求三棱錐
,求三棱錐![]() 的體積.
的體積.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,四棱錐P-ABCD中, PA⊥平面ABCD,E為BD的中點,G為PD的中點,△DAB≌△DCB,EA=EB=AB=1, ![]() ,連接CE并延長交AD于F.
,連接CE并延長交AD于F.
(Ⅰ)求證:AD⊥CG;
(Ⅱ)求平面BCP與平面DCP的夾角的余弦值.

查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】依據(jù)某地某條河流8月份的水文觀測點的歷史統(tǒng)計數(shù)據(jù)所繪制的頻率分布直方圖如圖(甲)所示;依據(jù)當?shù)氐牡刭|(zhì)構(gòu)造,得到水位與災(zāi)害等級的頻率分布條形圖如圖(乙)所示.
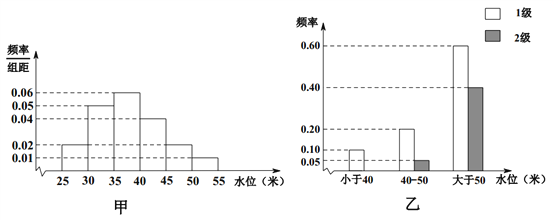
試估計該河流在8月份水位的中位數(shù);
(1)以此頻率作為概率,試估計該河流在8月份發(fā)生1級災(zāi)害的概率;
(2)該河流域某企業(yè),在8月份,若沒受1、2級災(zāi)害影響,利潤為500萬元;若受1級災(zāi)害影響,則虧損100萬元;若受2級災(zāi)害影響則虧損1000萬元.
現(xiàn)此企業(yè)有如下三種應(yīng)對方案:
方案 | 防控等級 | 費用(單位:萬元) |
方案一 | 無措施 | 0 |
方案二 | 防控1級災(zāi)害 | 40 |
方案三 | 防控2級災(zāi)害 | 100 |
試問,如僅從利潤考慮,該企業(yè)應(yīng)選擇這三種方案中的哪種方案?說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某種植園在芒果臨近成熟時,隨機從一些芒果樹上摘下100個芒果,其質(zhì)量分別在![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() (單位:克)中,經(jīng)統(tǒng)計得頻率分布直方圖如圖所示.
(單位:克)中,經(jīng)統(tǒng)計得頻率分布直方圖如圖所示.

(1)現(xiàn)按分層抽樣從質(zhì)量為![]() ,
,![]() 的芒果中隨機抽取
的芒果中隨機抽取![]() 個,再從這
個,再從這![]() 個中隨機抽取
個中隨機抽取![]() 個,記隨機變量
個,記隨機變量![]() 表示質(zhì)量在
表示質(zhì)量在![]() 內(nèi)的芒果個數(shù),求
內(nèi)的芒果個數(shù),求![]() 的分布列及數(shù)學期望.
的分布列及數(shù)學期望.
(2)以各組數(shù)據(jù)的中間數(shù)代表這組數(shù)據(jù)的平均值,將頻率視為概率,某經(jīng)銷商來收購芒果,該種植園中還未摘下的芒果大約還有![]() 個,經(jīng)銷商提出如下兩種收購方案:
個,經(jīng)銷商提出如下兩種收購方案:
A:所以芒果以![]() 元/千克收購;
元/千克收購;
B:對質(zhì)量低于![]() 克的芒果以
克的芒果以![]() 元/個收購,高于或等于
元/個收購,高于或等于![]() 克的以
克的以![]() 元/個收購.
元/個收購.
通過計算確定種植園選擇哪種方案獲利更多?
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】設(shè)函數(shù)![]() 的定義域為
的定義域為![]() ,若滿足條件:存在
,若滿足條件:存在![]() ,使
,使![]() 在
在![]() 上的值域為
上的值域為![]() ,則稱
,則稱![]() 為“倍縮函數(shù)”.若函數(shù)
為“倍縮函數(shù)”.若函數(shù)![]() 為“倍縮函數(shù)”,則實數(shù)
為“倍縮函數(shù)”,則實數(shù)![]() 的取值范圍是
的取值范圍是
A. (﹣∞,ln2﹣1) B. (﹣∞,ln2﹣1]
C. (1﹣ln2,+∞) D. [1﹣ln2,+∞)
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在直角坐標系中,曲線![]() 的參數(shù)方程為
的參數(shù)方程為![]() (
(![]() 為參數(shù),
為參數(shù),![]() ),在以坐標原點為極點,
),在以坐標原點為極點,![]() 軸非負軸為極軸的極坐標系中,曲線
軸非負軸為極軸的極坐標系中,曲線![]() :
:![]() (
(![]() 為極角).
為極角).
(1)將曲線![]() 化為極坐標方程,當
化為極坐標方程,當![]() 時,將
時,將![]() 化為直角坐標方程;
化為直角坐標方程;
(2)若曲線![]() 與
與![]() 相交于一點
相交于一點![]() ,求
,求![]() 點的直角坐標使
點的直角坐標使![]() 到定點
到定點![]() 的距離最小.
的距離最小.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com