
【題目】已知函數![]()
(1)當![]() 時,求曲線
時,求曲線![]() 在點
在點![]() 處的切線方程;
處的切線方程;
(2)當![]() 時,討論
時,討論![]() 的單調性.
的單調性.
【答案】(1)![]() ;(2)詳見解析.
;(2)詳見解析.
【解析】試題分析:本題主要考查導數的運算、利用導數求曲線的切線方程、利用導數求函數的單調性等基礎知識,考查學生的分析問題解決問題的能力、計算能力.第一問,先將![]() 代入得到
代入得到![]() 表達式,對
表達式,對![]() 求導,將切點的橫坐標2代入
求導,將切點的橫坐標2代入![]() 中得到切線的斜率k,再將切點的橫坐標2代入到
中得到切線的斜率k,再將切點的橫坐標2代入到![]() 中,得到切點的縱坐標,最后利用點斜式寫出切線方程;第二問,討論
中,得到切點的縱坐標,最后利用點斜式寫出切線方程;第二問,討論![]() 的單調性即討論
的單調性即討論![]() 的正負,即討論導數表達式分子的正負,所以構造函數
的正負,即討論導數表達式分子的正負,所以構造函數![]() ,通過分析題意,將
,通過分析題意,將![]() 分成
分成![]() 、
、![]() 、
、![]() 、
、![]() 多種情況,分類討論,判斷
多種情況,分類討論,判斷![]() 的正負,從而得到
的正負,從而得到![]() 的單調性.
的單調性.
試題解析:(1)當![]() 時,
時, ![]()
![]() 6分
6分
(2)因為![]() ,
,
所以![]()
![]()
![]() ,
,
令![]()
![]() 8分
8分
(i)當a=0時, ![]()
所以當![]() 時g(x)>0,
時g(x)>0, ![]() 此時函數
此時函數![]() 單調遞減,
單調遞減,
x∈(1,∞)時,g(x)<0, ![]() 此時函數f,(x)單調遞增。
此時函數f,(x)單調遞增。
(ii)當![]() 時,由
時,由![]() ,解得:
,解得: ![]() 10分
10分
①若![]() ,函數f(x)在
,函數f(x)在![]() 上單調遞減, 11分
上單調遞減, 11分
②若![]() ,在
,在![]() 單調遞減,在
單調遞減,在![]() 上單調遞增.
上單調遞增.
③ 當a<0時,由于1/a-1<0,
x∈(0,1)時,g(x)>0,此時![]() ,函數f(x)單調遞減;
,函數f(x)單調遞減;
x∈(1,∞)時,g(x)<0 , ![]() ,此時函數
,此時函數![]() 單調遞增。
單調遞增。
綜上所述:
當a≤ 0 時,函數f(x)在(0,1)上單調遞減;
函數f(x)在 (1, +∞) 上單調遞增
當![]() 時,函數f(x)在(0, + ∞)上單調遞減
時,函數f(x)在(0, + ∞)上單調遞減
當![]() 時,函數f(x)在
時,函數f(x)在![]() 上單調遞減;
上單調遞減;
函數 f(x)在![]() 上單調遞增; 14分
上單調遞增; 14分


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】公元263年左右,我國數學家劉徽發現當圓內接正多邊形的邊數無限增加時,多邊形的面積可無限接近圓的面積,并創立了“割圓術”,利用“割圓術”,劉徽得到了圓周率精確到小數點后兩位的近似值3.14,這就是著名的“徽率”,利用劉徽的“割圓術”思想設計的一個程序框圖,則輸出的值為( )
(參考數據: ![]() )
)
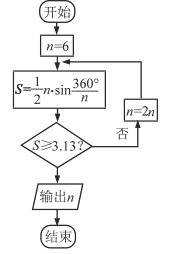
A. 12 B. 24 C. 48 D. 96
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,點
中,點![]() 的坐標為
的坐標為![]() ,直線
,直線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數).以坐標原點
為參數).以坐標原點![]() 為極點,以
為極點,以![]() 軸的非負半軸為極軸,選擇相同的單位長度建立極坐標系,圓
軸的非負半軸為極軸,選擇相同的單位長度建立極坐標系,圓![]() 極坐標方程為
極坐標方程為![]() .
.
(Ⅰ)當![]() 時,求直線
時,求直線![]() 的普通方程和圓
的普通方程和圓![]() 的直角坐標方程;
的直角坐標方程;
(Ⅱ)直線![]() 與圓
與圓![]() 的交點為
的交點為![]() 、
、![]() ,證明:
,證明:![]() 是與
是與![]() 無關的定值.
無關的定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,點
,點![]() 在橢圓
在橢圓![]() 上.
上.
(1)求橢圓![]() 的方程;
的方程;
(2)經過橢圓![]() 的右焦點
的右焦點![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 交于
交于![]() 、
、![]() 兩點,
兩點,![]() 、
、![]() 分別為橢圓
分別為橢圓![]() 的左、右頂點,記
的左、右頂點,記![]() 與
與![]() 的面積分別為
的面積分別為![]() 和
和![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
已知曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),以平面直角坐標系的原點為極點,
為參數),以平面直角坐標系的原點為極點,![]() 軸的正半軸為極軸建立極坐標系.
軸的正半軸為極軸建立極坐標系.
(1)求曲線![]() 的普通方程,并說明其表示什么軌跡;
的普通方程,并說明其表示什么軌跡;
(2)若直線![]() 的極坐標方程為
的極坐標方程為![]() ,試判斷直線
,試判斷直線![]() 與曲線
與曲線![]() 的位置關系,若相交,請求出其弦長.
的位置關系,若相交,請求出其弦長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
:![]()
![]() 的左焦點為
的左焦點為![]() ,上頂點為
,上頂點為![]() ,長軸長為
,長軸長為![]() ,
,![]() 為直線
為直線![]() :
:![]() 上的動點,
上的動點,![]() ,
,![]() .當
.當![]() 時,
時,![]() 與
與![]() 重合.
重合.
(1)若橢圓![]() 的方程;
的方程;
(2)若直線![]() 交橢圓
交橢圓![]() 于
于![]() ,
,![]() 兩點,若
兩點,若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com