
在三棱錐 中,側棱長均為
中,側棱長均為 ,底邊
,底邊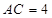 ,
, ,
, ,
,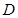 、
、 分別為
分別為 、
、 的中點.
的中點.
(1)求三棱錐 的體積;
的體積;
(2)求二面角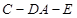 的平面角.
的平面角.
(1)三棱錐 的體積為
的體積為 ;(2)二面角
;(2)二面角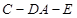 的平面角的大小為
的平面角的大小為 .
.
解析試題分析:(1)由于三棱錐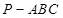 的側棱長都相等,可以得到點
的側棱長都相等,可以得到點 在平面
在平面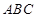 內的射影點為
內的射影點為 的外心,而由于
的外心,而由于 的三條底邊滿足勾股定理,可知
的三條底邊滿足勾股定理,可知 為直角三角形
為直角三角形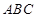 的斜邊,從而可以知道
的斜邊,從而可以知道 的中點
的中點 即為直角三角形
即為直角三角形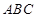 的外心,然后利用勾股定理求出
的外心,然后利用勾股定理求出 ,并且計算出直角三角形
,并且計算出直角三角形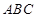 的面積,最后利用錐體的體積公式計算此三棱錐的體積;(2)解法一是在(1)中的基礎上,利用
的面積,最后利用錐體的體積公式計算此三棱錐的體積;(2)解法一是在(1)中的基礎上,利用 平面
平面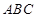 ,得到平面
,得到平面 平面
平面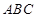 ,然后在平面
,然后在平面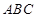 內作
內作 于點
于點 ,利用平面與平面垂直的性質定理得到
,利用平面與平面垂直的性質定理得到 平面
平面 ,從而得到
,從而得到 ,再從點
,再從點 在平面
在平面 內作
內作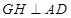 于點
于點 ,并連接
,并連接 ,利用三垂線法得到
,利用三垂線法得到 為二面角
為二面角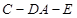 的平面角,最后在直角三角形
的平面角,最后在直角三角形 中計算
中計算 的大小;解法二是以
的大小;解法二是以 為原點,以
為原點,以 為
為 軸建立空間直角坐標系,利用空間向量法求二面角
軸建立空間直角坐標系,利用空間向量法求二面角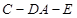 的平面角的大小.
的平面角的大小.
試題解析:(1)取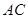 的中點
的中點 ,連接
,連接 ,
,
易得: ,
, ,
,  ,
, .
. .
.
又

 平面
平面 ,
,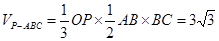
(2)法一:作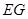 ⊥
⊥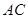 ,
, ⊥
⊥ 于
于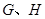 點,連接
點,連接

 平面
平面 ,
, 平面
平面 ,
,
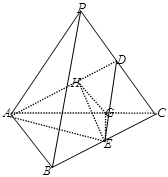
又

 平面
平面 .
.
∵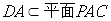 , ∴
, ∴
又

 平面
平面 ,
,
∵ ,∴
,∴ ,
,
∴


 口算題卡加應用題集訓系列答案
口算題卡加應用題集訓系列答案 綜合自測系列答案
綜合自測系列答案科目:高中數學 來源: 題型:解答題
如圖,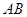 是圓柱體
是圓柱體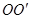 的一條母線,
的一條母線,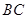 過底面圓的圓心
過底面圓的圓心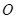 ,
,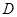 是圓
是圓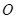 上不與點
上不與點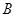 、
、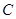 重合的任意一點,已知棱
重合的任意一點,已知棱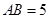 ,
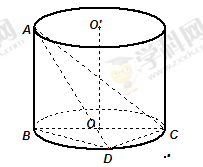
,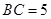 ,
,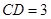 .
.
(1)求證: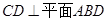 ;
;
(2)將四面體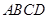 繞母線
繞母線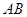 轉動一周,求
轉動一周,求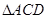 的三邊在旋轉過程中所圍成的幾何體的體積.
的三邊在旋轉過程中所圍成的幾何體的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖,正三棱柱ABC—A1B1C1的各棱長都相等,M、E分別是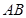 和AB1的中點,點F在BC上且滿足BF∶FC=1∶3.
和AB1的中點,點F在BC上且滿足BF∶FC=1∶3.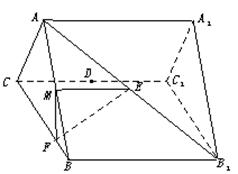
(1)求證:BB1∥平面EFM;
(2)求四面體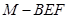 的體積.
的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖,直三棱柱ABC-A1B1C1中,D,E分別是AB,BB1的中點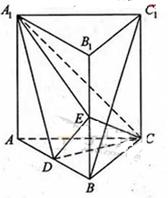
(Ⅰ)證明:BC1//平面A1CD;
(Ⅱ)設AA1=AC=CB=2,AB=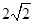 ,求三棱錐C一A1DE的體積.
,求三棱錐C一A1DE的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖,在三棱柱ABC-A1B1C1中,A1B⊥平面ABC,AB⊥AC.
(1)求證:AC⊥BB1;
(2)若P是棱B1C1的中點,求平面PAB將三棱柱分成的兩部分體積之比.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某高速公路收費站入口處的安全標識墩如圖1所示。墩的上半部分是正四棱錐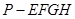 ,下半部分是長方體
,下半部分是長方體 。圖2、圖3分別是該標識墩的正(主)視圖和俯視圖。
。圖2、圖3分別是該標識墩的正(主)視圖和俯視圖。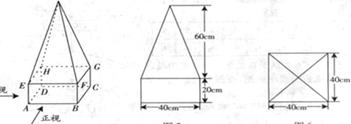
圖1 圖2 圖3
(1)請在正視圖右側畫出該安全標識墩的側(左)視圖;
(2)求該安全標識墩的體積;
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com