
【題目】在平面直角坐標(biāo)系![]() 中,橢圓E:
中,橢圓E:![]() (
(![]() )的長軸長為4,左準(zhǔn)線l的方程為
)的長軸長為4,左準(zhǔn)線l的方程為![]() .
.
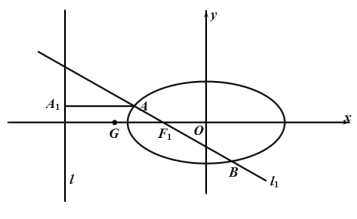
(1)求橢圓的標(biāo)準(zhǔn)方程;
(2)直線![]() 過橢圓E的左焦點
過橢圓E的左焦點![]() ,且與橢圓E交于A,B兩點.
,且與橢圓E交于A,B兩點.
①若![]() ,求直線
,求直線![]() 的方程;
的方程;
②過A作左準(zhǔn)線l的垂線,垂足為![]() ,點
,點![]() ,求證:
,求證:![]() ,B,G三點共線.
,B,G三點共線.
【答案】(1)![]() (2)①
(2)①![]() 或
或![]() ,②證明見解析
,②證明見解析
【解析】
(1)根據(jù)長軸的值和準(zhǔn)線的方程,可求得![]() ,
,![]() 的值,結(jié)合
的值,結(jié)合![]() ,從而可求出橢圓的標(biāo)準(zhǔn)方程;
,從而可求出橢圓的標(biāo)準(zhǔn)方程;
(2)①設(shè)![]() ,
,![]() ,作
,作![]() ,根據(jù)橢圓的第二定義可得
,根據(jù)橢圓的第二定義可得![]() ,結(jié)合
,結(jié)合![]() ,可推出
,可推出![]() ,從而推出
,從而推出![]() ,根據(jù)
,根據(jù)![]() ,可得
,可得![]() ,分別對直線
,分別對直線![]() 的斜率存在與不存在進行討論,結(jié)合韋達定理即可求得直線
的斜率存在與不存在進行討論,結(jié)合韋達定理即可求得直線![]() 的方程;
的方程;
②當(dāng)直線![]() 的斜率不存在時,分別求出
的斜率不存在時,分別求出![]() ,
,![]() ,即可得證;當(dāng)直線
,即可得證;當(dāng)直線![]() 的斜率存在時,分別求出
的斜率存在時,分別求出![]() ,
,![]() ,結(jié)合韋達定理即可求證.
,結(jié)合韋達定理即可求證.
(1)由題,![]() ,
,![]() ,∴
,∴![]() ,
,![]()
∴![]() ,橢圓方程
,橢圓方程![]() .
.
(2)①設(shè)![]() ,
,![]()
作![]() ,由第二定義,
,由第二定義,![]() ,而
,而![]()
∴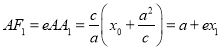 ,同理
,同理![]()
∴![]() ,即
,即![]() ,②證明見解析
,②證明見解析
設(shè)![]() 的斜率為k
的斜率為k
1°若k不存在,即![]() (舍)
(舍)
2°若k存在,![]() :
:![]()
聯(lián)立
消去y,![]() (*),
(*),![]() 恒成立
恒成立
∴![]() ,即
,即![]() ,∴
,∴![]() :
:![]() 或
或![]()
②證明1°若![]() 的斜率不存在,
的斜率不存在,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
∴![]() ,B,G三點共線.
,B,G三點共線.
2°若![]() 的斜率存在,
的斜率存在,![]() ,
,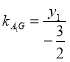 ,
,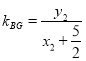
要證![]() ,B,G共線.即證
,B,G共線.即證![]() ,即
,即![]() ,即
,即![]()
即![]() ,即
,即![]()
由(*)![]() ,
,![]()
代入上式:![]() ,即
,即![]() 顯然成立。
顯然成立。
∴![]() ,B,G三點共線.
,B,G三點共線.
綜上所述,![]() ,B,G三點共線.
,B,G三點共線.


科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() ,
,![]() .
.
(1)若![]() ,判斷函數(shù)
,判斷函數(shù)![]() 的單調(diào)性并說明理由;
的單調(diào)性并說明理由;
(2)若![]() ,求證:關(guān)
,求證:關(guān)![]() 的不等式
的不等式![]() 在
在![]() 上恒成立.
上恒成立.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)![]() 為常數(shù),函數(shù)
為常數(shù),函數(shù)![]() ,給出以下結(jié)論:
,給出以下結(jié)論:
(1)若![]() ,則
,則![]() 存在唯一零點
存在唯一零點
(2)若![]() ,則
,則![]()
(3)若![]() 有兩個極值點
有兩個極值點![]() ,則
,則![]()
其中正確結(jié)論的個數(shù)是( )
A. 3B. 2C. 1D. 0
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】“![]() 猜想”是指對于每一個正整數(shù)
猜想”是指對于每一個正整數(shù)![]() ,若
,若![]() 為偶數(shù),則讓它變成
為偶數(shù),則讓它變成![]() ;若
;若![]() 為奇數(shù),則讓它變成
為奇數(shù),則讓它變成![]() .如此循環(huán),最終都會變成
.如此循環(huán),最終都會變成![]() ,若數(shù)字
,若數(shù)字![]() 按照以上的規(guī)則進行變換,則變換次數(shù)為偶數(shù)的頻率是( )
按照以上的規(guī)則進行變換,則變換次數(shù)為偶數(shù)的頻率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖①,是由矩形![]() ,
,![]() 和
和![]() 組成的一個平面圖形,其中
組成的一個平面圖形,其中![]() ,
,![]() ,將其沿
,將其沿![]() 折起使得
折起使得![]() 重合,連接
重合,連接![]() 如圖②.
如圖②.
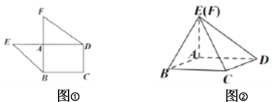
(1)證明:平面![]() 平面
平面![]() ;
;
(2)若![]() 為線段
為線段![]() 中點,求直線
中點,求直線![]() 與平面
與平面![]() 所成角的正切值.
所成角的正切值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知數(shù)列![]() 的前
的前![]() 項和為
項和為![]() ,
,![]() ,
,![]() (
(![]() 且
且![]() ),數(shù)列
),數(shù)列![]() 滿足:
滿足:![]() ,且
,且![]() (
(![]() 且
且![]() ).
).
(Ⅰ)求數(shù)列![]() 的通項公式;
的通項公式;
(Ⅱ)求證:數(shù)列![]() 為等比數(shù)列;
為等比數(shù)列;
(Ⅲ)求數(shù)列![]() 的前
的前![]() 項和的最小值.
項和的最小值.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com