
���}Ŀ���O(sh��)�E�A![]() �����ҽ��c(di��n)�քe��
�����ҽ��c(di��n)�քe��![]() ��
��![]() ������c(di��n)��
������c(di��n)��![]() ��
��![]() ������(bi��o)ԭ�c(di��n)���c(di��n)
������(bi��o)ԭ�c(di��n)���c(di��n)![]() ��ֱ��
��ֱ��![]() �ľ��x��
�ľ��x��![]() ��
��![]() �����ֱ��������.
�����ֱ��������.
��1����E�A![]() �Ę�(bi��o)��(zh��n)���̣�
�Ę�(bi��o)��(zh��n)���̣�
��2��ֱ��![]() �c�E�A
�c�E�A![]() ����
����![]() ��
��![]() ���c(di��n)����ֱ��
���c(di��n)����ֱ��![]() �cֱ��
�cֱ��![]() ��б��֮�͞�
��б��֮�͞�![]() ���C����ֱ��
���C����ֱ��![]() ���^���c(di��n)�������ԓ���c(di��n)������(bi��o).
���^���c(di��n)�������ԓ���c(di��n)������(bi��o).
���𰸡���1��![]() ����2��Ҋ����
����2��Ҋ����
��������
��1������![]() ��ʾ���c(di��n)
��ʾ���c(di��n)![]() ��ֱ��
��ֱ��![]() �ľ��x��������
�ľ��x��������![]() ��
��![]() ���P(gu��n)ϵ�õ����̣����õ���(bi��o)��(zh��n)���̣���2����(d��ng)ֱ��
���P(gu��n)ϵ�õ����̣����õ���(bi��o)��(zh��n)���̣���2����(d��ng)ֱ��![]() б�ʴ��ڕr�����O(sh��)ֱ�����̣�����б��֮�͞�
б�ʴ��ڕr�����O(sh��)ֱ�����̣�����б��֮�͞�![]() �õ�
�õ�![]() �c
�c![]() ���P(gu��n)ϵ����ֱ�����̻���
���P(gu��n)ϵ����ֱ�����̻���![]() ���Ķ��õ����c(di��n)����(d��ng)б�ʲ����ڕr���l(f��)�F(xi��n)ֱ��Ҳ�^ԓ���c(di��n)���Ķ���ýY(ji��)��.
���Ķ��õ����c(di��n)����(d��ng)б�ʲ����ڕr���l(f��)�F(xi��n)ֱ��Ҳ�^ԓ���c(di��n)���Ķ���ýY(ji��)��.
��1���⣺���}���֪��ֱ��![]() �ķ��̞�
�ķ��̞�![]() ����
����![]()
�t![]()
��?y��n)?/span>![]() �����ֱ�������Σ�����
�����ֱ�������Σ�����![]()
��![]()
�ɽ��![]() ��
��![]() ��
��![]()
���ԙE�A![]() �Ę�(bi��o)��(zh��n)���̞�
�Ę�(bi��o)��(zh��n)���̞�![]()
��2���C�����ɣ�1��֪![]()
��(d��ng)ֱ��![]() ��б�ʴ��ڕr���O(sh��)ֱ��
��б�ʴ��ڕr���O(sh��)ֱ��![]() �ķ��̞�
�ķ��̞�![]()
����![]() ����
����![]()
����![]() ����
����![]()
�O(sh��)![]() ��
��![]() ���t
���t![]() ��
��![]()
��?y��n)�ֱ��![]() �cֱ��
�cֱ��![]() ��б��֮�͞�
��б��֮�͞�![]()
����![]()
![]()
������![]()
����ֱ��![]() �ķ��̞�
�ķ��̞�![]()
�@Ȼֱ��![]() ��(j��ng)�^���c(di��n)
��(j��ng)�^���c(di��n)![]()
��(d��ng)ֱ��![]() ��б�ʲ����ڕr���O(sh��)ֱ��
��б�ʲ����ڕr���O(sh��)ֱ��![]() �ķ��̞�
�ķ��̞�![]()
��?y��n)�ֱ��![]() �cֱ����б��֮�͞�
�cֱ����б��֮�͞�![]() ���O(sh��)
���O(sh��)![]() ���t
���t![]()
����![]() �����
�����![]()
�˕rֱ��![]() �ķ��̞�
�ķ��̞�![]()
�@Ȼֱ��![]() Ҳ��(j��ng)�^ԓ���c(di��n)
Ҳ��(j��ng)�^ԓ���c(di��n)![]()
�C�ϣ�ֱ��![]() ���^�c(di��n)
���^�c(di��n)![]()



| �꼉 | �����n�� | �꼉 | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����ƽ��ֱ������(bi��o)ϵ![]() �У��A
�У��A![]() �ą���(sh��)���̞�
�ą���(sh��)���̞�![]() ��
��![]() �酢��(sh��)�����^�c(di��n)
�酢��(sh��)�����^�c(di��n)![]() ��б�ʞ�
��б�ʞ�![]() ��ֱ��
��ֱ��![]() �c�A
�c�A![]() ����
����![]() ��
��![]() ���c(di��n).
���c(di��n).
��1����A��![]() ��ֱ��
��ֱ��![]() �ľ��x��
�ľ��x��![]() ����
����![]() ��ֵ��
��ֵ��
��2����![]() ���c(di��n)
���c(di��n)![]() ��܉�E����.
��܉�E����.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ���ڔ�(sh��)�W(xu��)��ģ�n�ϣ��ώ��o���?gu��)�����һ�t������2019��8��16�����磬423�Ė|ݸ��һ�ߘ���ӯ���Q(m��o)����2̖�ǣ����º��Q�����Q(m��o)����������ʽ��픣��S�����һ��������������λ����(bi��o)־���|ݸ��ߘǼo(j��)��Q�����ɖ|ݸ���غ�ĸ����I(y��)��ӯ���F(tu��n)ˢ���˖|ݸ���H������֮ǰ�Ė|ݸ��һ�ߘ��_�̴�B�߳�134��.����ͬ�W(xu��)�����@�@�У��ώ�����ˆ��}�����Q(m��o)���������@ô�߆�҂��ܷ��\(y��n)�����W(xu��)֪�R�y���(y��n)�Cһ�£�һ�ܺɂ��dȤС�M�������������ԵĜy������.
��һС�M���õ������ɴΜy�Ƿ����������ڇ��Q(m��o)���ĸ��ڵĕ�չ���ďV���ϵ�![]() �c(di��n)�y�Ç��Q(m��o)����픲������Ǟ�
�c(di��n)�y�Ç��Q(m��o)����픲������Ǟ�![]() ���������Q(m��o)����ǰ�M(j��n)��
���������Q(m��o)����ǰ�M(j��n)��![]() ���_(d��)
���_(d��)![]() �c(di��n)����
�c(di��n)����![]() �c(di��n)�y�Ç��Q(m��o)����픲������Ǟ�
�c(di��n)�y�Ç��Q(m��o)����픲������Ǟ�![]() ��Ȼ��Ӌ(j��)������Q(m��o)���ĵĸ߶ȣ���D��.
��Ȼ��Ӌ(j��)������Q(m��o)���ĵĸ߶ȣ���D��.
�ڶ�С�M���õ������R�淴�䷨�����ڇ��Q(m��o)���ĺ���������o(j��)���@һ��11�Әǣ��c���Q(m��o)����̎��ͬһˮƽ�棬ÿ�Ӽs3�ף�������_�ϣ��M(j��n)�Ѓɂ��������E���ٌ�ƽ���R�������_�����ϣ��˺��������R���ܿ������Q(m��o)��B��픲�λ�ã��y�������c�R�ӵľ��x��![]() �ף����������Q(m��o)���ģ����R��ǰ��
�ף����������Q(m��o)���ģ����R��ǰ��![]() �ף��؏�(f��)���еIJ������y�������c�R�ӵľ��x��
�ף��؏�(f��)���еIJ������y�������c�R�ӵľ��x��![]() ��.Ȼ��Ӌ(j��)������Q(m��o)���ĵĸ߶ȣ���D��.
��.Ȼ��Ӌ(j��)������Q(m��o)���ĵĸ߶ȣ���D��.
��(sh��)�H�����У���һС�M�y��![]() �ף�
�ף�![]() ��
��![]() ����K��Ç��Q(m��o)���ĸ߶Ȟ�
����K��Ç��Q(m��o)���ĸ߶Ȟ�![]() ���ڶ�С�M�y��
���ڶ�С�M�y��![]() �ף�
�ף�![]() �ף�
�ף�![]() �ף���K��Ç��Q(m��o)���ĸ߶Ȟ�
�ף���K��Ç��Q(m��o)���ĸ߶Ȟ�![]() �����O(sh��)�����y���ߵ����۸�
�����O(sh��)�����y���ߵ����۸�![]() ������
������![]() ��.
��.
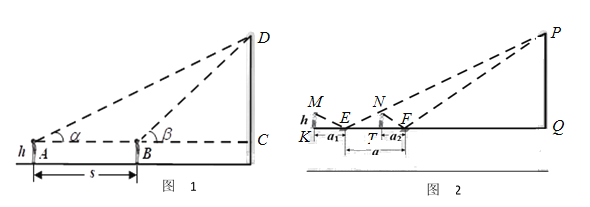
��1��Ո�������W(xu��)֪�R�̓ɂ�С�M���Ӌ(j��)�㣨������(sh��)��(j��)��![]() ��
��![]() ,�𰸱�������(sh��)�Y(ji��)������
,�𰸱�������(sh��)�Y(ji��)������
��2�����J(r��n)���Ă�С�M�ķ������ã��f���������.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����1����(d��ng)![]() �r������ʽ
�r������ʽ![]() ���������(sh��)��(sh��)
���������(sh��)��(sh��)![]() ��ȡֵ������
��ȡֵ������
��2����֪����(sh��)![]() ��
��![]() ���������(sh��)
���������(sh��)![]() �Ѓɂ��Oֵ�c(di��n)
�Ѓɂ��Oֵ�c(di��n)![]() ��
��![]() �����C��
�����C��![]() .��������(sh��)��(j��)��
.��������(sh��)��(j��)��![]() ��
��![]() ��
��![]() ��
��![]() ����Ȼ����(sh��)�ĵה�(sh��)��
����Ȼ����(sh��)�ĵה�(sh��)��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����ƽ��ֱ������(bi��o)ϵ![]() �У�����
������![]() ��
��![]() ��
��![]() �酢��(sh��)��.����
�酢��(sh��)��.����![]() ��ԭ�c(di��n)��
��ԭ�c(di��n)�� ![]() �S�����S��O�S�ĘO����(bi��o)ϵ�У�����
�S�����S��O�S�ĘO����(bi��o)ϵ�У�����![]() �ĘO����(bi��o)���̞�
�ĘO����(bi��o)���̞�![]() ���侀
���侀![]() �c
�c![]() ���O�c(di��n)���һ�����c(di��n)��
���O�c(di��n)���һ�����c(di��n)��![]() ���O(sh��)ֱ��
���O(sh��)ֱ��![]() ��(j��ng)�^�c(di��n)
��(j��ng)�^�c(di��n)![]() ���҃Aб�Ǟ�
���҃Aб�Ǟ�![]() ��ֱ��
��ֱ��![]() �c����
�c����![]() �ăɂ����c(di��n)��
�ăɂ����c(di��n)��![]() .
.
��1����![]() ����ͨ���̺�
����ͨ���̺�![]() ��ֱ������(bi��o)���̣�
��ֱ������(bi��o)���̣�
��2����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ��܊Ӗ(x��n)�r���ס��҃���ͬ�W(xu��)�M(j��n)�������ِ������ِ10����ÿ����ِ������ĴΣ�����ÿ�����Эh(hu��n)��(sh��)֮������ԓ����ِ�ijɿ���?d��ng)?sh��)�W(xu��)�ώ����ס��҃���ͬ�W(xu��)��10����ِ�ɿ��L����D��ʾ���o�~�D�����o������4���Y(ji��)Փ��(1)��ƽ���ɿ����ҵ�ƽ���ɿ��ߣ�(2)�ijɿ��ĘO����29��(3)�ҵijɿ��ı���(sh��)��21��(4)�ҵijɿ�����λ��(sh��)��18���t�@4���Y(ji��)Փ�У����_�Y(ji��)Փ�Ă���(sh��)��(����)

A. 1B. 2C. 3D. 4
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ��ij��˾Ӌ(j��)��ُ�I2�_�C(j��)����ԓ�N�C(j��)��ʹ���������̭.�C(j��)����һ�דp�������ُ�M(j��n)�C(j��)���r�������~��ُ�I�@�N�����������ÿ��200Ԫ.�ڙC(j��)��ʹ�����g��������������ُ�I���tÿ��500Ԫ.�F(xi��n)��Q����ُ�I�C(j��)���r��(y��ng)ͬ�rُ�I�ׂ��דp���������Ѽ���������100�_�@�N�C(j��)��������ʹ���ڃ�(n��i)���Q���דp�����(sh��)������������D��

���@100�_�C(j��)�����Q���דp�����(sh��)���l�ʴ���1�_�C(j��)�����Q���דp�����(sh��)�l(f��)���ĸ��ʣ�ӛ![]() ��ʾ2�_�C(j��)�������(n��i)������Q���דp�����(sh��)��
��ʾ2�_�C(j��)�������(n��i)������Q���דp�����(sh��)��![]() ��ʾُ�I2�_�C(j��)����ͬ�rُ�I���דp�����(sh��).
��ʾُ�I2�_�C(j��)����ͬ�rُ�I���דp�����(sh��).
��������![]() �ķֲ��У�
�ķֲ��У�
��������Ҫ��![]() ���_��
���_��![]() ����Сֵ��
����Сֵ��
��������ُ�I�דp��������M(f��i)�õ�����ֵ��Q������(j��)����![]() �c
�c![]() ֮���x��һ����(y��ng)�x���Ă���
֮���x��һ����(y��ng)�x���Ă���
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ���������}�����_���ǣ� ��
A.![]() �ǿ��g�е����c(di��n)����
�ǿ��g�е����c(di��n)����![]() ���ܘ�(g��u)�ɿ��g���ף��t
���ܘ�(g��u)�ɿ��g���ף��t![]() ����
����
B.��֪![]() ����g��һ�����ף���
����g��һ�����ף���![]() ���t
���t![]() Ҳ�ǿ��g�Ļ���
Ҳ�ǿ��g�Ļ���
C.��ֱ��![]() �ķ���������
�ķ���������![]() ��ƽ��
��ƽ��![]() �ķ�������
�ķ�������![]() ���tֱ��
���tֱ��![]()
D.��ֱ��![]() �ķ���������
�ķ���������![]() ��ƽ��
��ƽ��![]() �ķ�������
�ķ�������![]() ���tֱ��
���tֱ��![]() �cƽ��
�cƽ��![]() ���ɽǵ�����ֵ��
���ɽǵ�����ֵ��![]()
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]() .
.
������(sh��)![]() ���{(di��o)�^(q��)�g��
���{(di��o)�^(q��)�g��
������![]() ���������(sh��)��(sh��)
���������(sh��)��(sh��)![]() ��ȡֵ����.
��ȡֵ����.
�鿴�𰸺ͽ���>>
���H�W(xu��)У��(y��u)�x - ����(x��)���б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_ | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com