
【題目】在直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為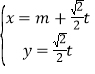 (
(![]() 為參數),以坐標原點
為參數),以坐標原點![]() 為極點,
為極點,![]() 軸正半軸為極軸建立極坐標系,橢圓
軸正半軸為極軸建立極坐標系,橢圓![]() 的極坐標方程為
的極坐標方程為![]() ,其左焦點
,其左焦點![]() 在直線
在直線![]() 上.
上.
(1)若直線![]() 與橢圓
與橢圓![]() 交于
交于![]() 兩點,求
兩點,求![]() 的值;
的值;
(2)求橢圓![]() 的內接矩形面積的最大值.
的內接矩形面積的最大值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)將參數方程化為直角坐標方程可得F的坐標為(![]() ,0),聯立直線的參數方程與橢圓方程,結合參數的幾何意義計算可得
,0),聯立直線的參數方程與橢圓方程,結合參數的幾何意義計算可得![]() .
.
(2)結合橢圓方程,設橢圓C上在第一象限內的任意一點M的坐標為(![]() ,4sinθ)(
,4sinθ)(![]() ),據此可得內接矩形關于
),據此可得內接矩形關于![]() 的面積函數,結合三角函數的性質即可確定面積S取得最大值.
的面積函數,結合三角函數的性質即可確定面積S取得最大值.
(1)將![]() 代入ρ2cos2θ+3ρ2sin2θ=48,
代入ρ2cos2θ+3ρ2sin2θ=48,
得x2+3y2=48,即![]() ,
,
因為c2=48-16=32,所以F的坐標為(![]() ,0),
,0),
又因為F在直線l上,所以![]() .
.
把直線l的參數方程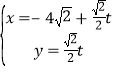 代入x2+3y2=48,
代入x2+3y2=48,
化簡得t2-4t-8=0,所以t1+t2=4,t1t2=-8,
所以![]() .
.
(2)由橢圓C的方程![]() ,可設橢圓C上在第一象限內的任意一點M的坐標為(
,可設橢圓C上在第一象限內的任意一點M的坐標為(![]() ,4sinθ)(
,4sinθ)(![]() ),
),
所以內接矩形的面積![]() ,
,
當![]() 時,面積S取得最大值
時,面積S取得最大值![]() .
.


 同步練習河南大學出版社系列答案
同步練習河南大學出版社系列答案 同步練習西南大學出版社系列答案
同步練習西南大學出版社系列答案科目:高中數學 來源: 題型:
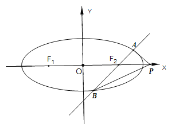
【題目】如圖,橢圓![]() :
:![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,橢圓
,橢圓![]() 上一點與兩焦點構成的三角形的周長為
上一點與兩焦點構成的三角形的周長為![]() ,離心率為
,離心率為![]() .
.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)過點![]() 的直線
的直線![]() 交橢圓
交橢圓![]() 于
于![]() 兩點,問在
兩點,問在![]() 軸上是否存在定點
軸上是否存在定點![]() ,使得
,使得![]() 為定值?證明你的結論.
為定值?證明你的結論.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某企業欲做一個介紹企業發展史的銘牌,銘牌的截面形狀是如圖所示的扇形環面(由扇形![]() 挖去扇形
挖去扇形![]() 后構成的).已知
后構成的).已知![]() ,線段
,線段![]() 與弧
與弧![]() 、弧
、弧![]() 的長度之和為
的長度之和為![]() 米,圓心角為
米,圓心角為![]() 弧度.
弧度.

(1)求![]() 關于
關于![]() 的函數解析式;
的函數解析式;
(2)記銘牌的截面面積為![]() ,試問
,試問![]() 取何值時,
取何值時,![]() 的值最大?并求出最大值.
的值最大?并求出最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】給出下列命題:
①已知![]() ,
,![]() 是正數,且
是正數,且![]() ,則
,則![]() ;
;
②命題“![]() ,使得
,使得![]() ”的否定是真命題;
”的否定是真命題;
③將![]() 化成二進位制數是
化成二進位制數是![]() ;
;
④某同學研究變量![]() ,
,![]() 之間的相關關系,并求得回歸直線方程,他得出一個結論:
之間的相關關系,并求得回歸直線方程,他得出一個結論:![]() 與
與![]() 負相關且
負相關且![]() ,
,
其中正確的命題的序號是__________(把你認為正確的序號都填上).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某地區工會利用“健步行![]() ”開展明年健步走積分獎勵活動.會員每天走5千步可獲積分30分(不足5千步不積分),每多走2千步再積20分(不足2千步不積分).為了解會員的健步走情況,工會在某天從系統中隨機抽取了1000名會員,統計了當天他們的步數,并將樣本數據分為
”開展明年健步走積分獎勵活動.會員每天走5千步可獲積分30分(不足5千步不積分),每多走2千步再積20分(不足2千步不積分).為了解會員的健步走情況,工會在某天從系統中隨機抽取了1000名會員,統計了當天他們的步數,并將樣本數據分為![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 九組,整理得到如下頻率分布直方圖:
九組,整理得到如下頻率分布直方圖:
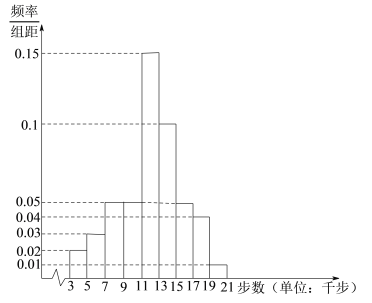
(1)從當天步數在![]() ,
,![]() ,
,![]() 的會員中按分層抽樣的方式抽取6人,再從這6人中隨機抽取2人,求這2人積分之和不少于220分的概率;
的會員中按分層抽樣的方式抽取6人,再從這6人中隨機抽取2人,求這2人積分之和不少于220分的概率;
(2)求該組數據的中位數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓C經過點![]() ,
,![]() ,且圓心在直線
,且圓心在直線![]() 上
上
(1)求圓C的方程.
(2)過點![]() 的直線與圓C交于A,B兩點,問:在直線
的直線與圓C交于A,B兩點,問:在直線![]() 上是否存在定點N,使得
上是否存在定點N,使得![]() (
(![]() ,
,![]() 分別為直線AN,BN的斜率)恒成立?若存在,請求出點N的坐標;若不存在,請說明理由.
分別為直線AN,BN的斜率)恒成立?若存在,請求出點N的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設集合A={1,2,…,2016}.對于A的任一個1008元子集X,若存在x、y∈X,滿足x<y,x|y,則稱X為“好集”.求最大的正整數a(a∈A),使得任一個含a的1008元子集皆為好集。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數y=a-bcos![]() (b>0)的最大值為
(b>0)的最大值為![]() ,最小值為-
,最小值為-![]() .
.
(1)求a,b的值;
(2)求函數g(x)=-4asin![]() 的最小值并求出對應x的集合.
的最小值并求出對應x的集合.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com