
【題目】![]() 是等邊三角形,邊長為4,
是等邊三角形,邊長為4, ![]() 邊的中點為
邊的中點為![]() ,橢圓
,橢圓![]() 以
以![]() ,
, ![]() 為左、右兩焦點,且經過
為左、右兩焦點,且經過![]() 、
、![]() 兩點。
兩點。
(1)求該橢圓的標準方程;
(2)過點![]() 且
且![]() 軸不垂直的直線
軸不垂直的直線![]() 交橢圓于
交橢圓于![]() ,
, ![]() 兩點,求證:直線
兩點,求證:直線![]() 與
與![]() 的交點在一條定直線上.
的交點在一條定直線上.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
: ![]() 的上下兩個焦點分別為
的上下兩個焦點分別為![]() ,
, ![]() ,過點
,過點![]() 與
與![]() 軸垂直的直線交橢圓
軸垂直的直線交橢圓![]() 于
于![]() 、
、![]() 兩點,
兩點, ![]() 的面積為
的面積為![]() ,橢圓
,橢圓![]() 的離心力為
的離心力為![]() .
.
(Ⅰ)求橢圓![]() 的標準方程;
的標準方程;
(Ⅱ)已知![]() 為坐標原點,直線
為坐標原點,直線![]() :
: ![]() 與
與![]() 軸交于點
軸交于點![]() ,與橢圓
,與橢圓![]() 交于
交于![]() ,
, ![]() 兩個不同的點,若存在實數
兩個不同的點,若存在實數![]() ,使得
,使得![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某市需對某環城快速車道進行限速,為了調研該道路車速情況,于某個時段隨機對![]() 輛車的速度進行取樣,測量的車速制成如下條形圖:
輛車的速度進行取樣,測量的車速制成如下條形圖:
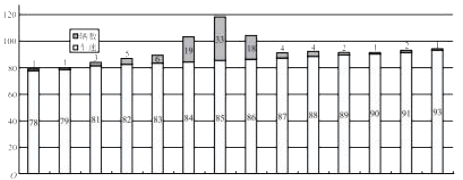
經計算:樣本的平均值![]() ,標準差
,標準差![]() ,以頻率值作為概率的估計值.已知車速過慢與過快都被認為是需矯正速度,現規定車速小于
,以頻率值作為概率的估計值.已知車速過慢與過快都被認為是需矯正速度,現規定車速小于![]() 或車速大于
或車速大于![]() 是需矯正速度.
是需矯正速度.
(1)從該快速車道上所有車輛中任取![]() 個,求該車輛是需矯正速度的概率;
個,求該車輛是需矯正速度的概率;
(2)從樣本中任取![]() 個車輛,求這
個車輛,求這![]() 個車輛均是需矯正速度的概率;
個車輛均是需矯正速度的概率;
(3)從該快速車道上所有車輛中任取![]() 個,記其中是需矯正速度的個數為
個,記其中是需矯正速度的個數為![]() ,求
,求![]() 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(本小題滿分為14分)已知定義域為R的函數![]() 是奇函數.
是奇函數.
(1)求a,b的值;
(2)若對任意的t∈R,不等式f(t2-2t)+f(2t2-k)<0恒成立,求k的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲、乙兩人為了響應政府“節能減排”的號召,決定各購置一輛純電動汽車.經了解目前市場上銷售的主流純電動汽車,按續駛里程數![]() (單位:公里)可分為三類車型,
(單位:公里)可分為三類車型, ![]() ,
, ![]() .甲從
.甲從![]() 三類車型中挑選,乙從
三類車型中挑選,乙從![]() 兩類車型中挑選,甲、乙兩人選擇各類車型的概率如表:
兩類車型中挑選,甲、乙兩人選擇各類車型的概率如表:
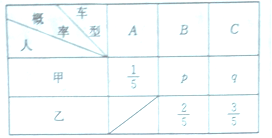
已知甲、乙都選![]() 類型的概率為
類型的概率為![]() .
.
(1)求![]() 的值;
的值;
(2)求甲、乙選擇不同車型的概率;
(3)某市對購買純電動汽車進行補貼,補貼標準如下表:

記甲、乙兩人購車所獲得的財政補貼之和為![]() ,求
,求![]() 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】現有一張長為![]() ,寬為
,寬為![]() (
(![]() )的長方形鐵皮
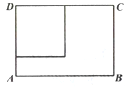
)的長方形鐵皮![]() ,準備用它做成一個無蓋長方體鐵皮容器,要求材料利用率為100%,不考慮焊接處損失.如圖,在長方形
,準備用它做成一個無蓋長方體鐵皮容器,要求材料利用率為100%,不考慮焊接處損失.如圖,在長方形![]() 的一個角上剪下一塊邊長為
的一個角上剪下一塊邊長為![]() 的正方形鐵皮,作為鐵皮容器的底面,用余下材料剪拼后作為鐵皮容器的側面,設長方體的高為
的正方形鐵皮,作為鐵皮容器的底面,用余下材料剪拼后作為鐵皮容器的側面,設長方體的高為![]() ,體積為
,體積為![]() .
.
(Ⅰ)求![]() 關于
關于![]() 的函數關系式;
的函數關系式;
(Ⅱ)求該鐵皮容器體積![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知某商品的進貨單價為1元/件,商戶甲往年以單價2元/件銷售該商品時,年銷量為1萬件.今年擬下調銷售單價以提高銷量增加收益.據估算,若今年的實際銷售單價為![]() 元/件(
元/件(![]() ),則新增的年銷量
),則新增的年銷量![]() (萬件).
(萬件).
(1)寫出今年商戶甲的收益![]() (單位:萬元)與
(單位:萬元)與![]() 的函數關系式;
的函數關系式;
(2)商戶甲今年采取降低單價提高銷量的營銷策略,是否能獲得比往年更大的收益(即比往年收益更多)?請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com