分析:解:(1)當a=100時,由題意知數列{a
n}的前34項成首項為100,公差為-3的等差數列,從第35項開始,奇數項均為3,偶數項均為1,由此能完成表格.
(2)當a=100時,由題意知數列{a
n}的前34項成首項為100,公差為-3的等差數列,從第35項開始,奇數項均為3,偶數項均為1,從而S
100=(100+97+94+…+4+1)+(3+1+…+3+1)(前一組共34項,后一組共66項),由此能求出結果.
(3)當
1<a<時,因為
an=,所以
bn==,由此能夠證明當
1<a<時,
Tn<.
解答:解:(1)
| n |
2 |
3 |
35 |
100 |
| an |
97 |
94 |
3 |
1 |
(2)當a=100時,由題意知數列{a
n}的前34項成首項為100,公差為-3的等差數列,從第35項開始,奇數項均為3,偶數項均為1,
從而S
100=(100+97+94+…+4+1)+(3+1+…+3+1)(前一組共34項,后一組共66項)
=
+(3+1)×=1717+132
=1849.
(3)當
1<a<時,因為
an=,
所以
bn==,
當n=2k,k∈N
*時,
T
n=b
1+b
2+…+b
2k=
-+-++…-+=-
(++…+)+(++…+)=-
+=
[1-()k].
因為1<a<
,所以
[1-()k]<,
當n=2k-1,k∈N
*時,
T
n=b
1+b
2+…+b
2k-1=
-+-++…-<
-+-++…-+<.
所以
Tn<.
點評:本題考查數列與函數的綜合運用.解題時要認真審題,注意挖掘題設中的隱含條件,合理地進行等價轉化.本題的易錯點是不區分n的奇偶性,導致出錯.




 ,
,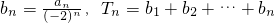 ,求證:當
,求證:當 時,
時,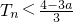 .
.