
【題目】已知函數(shù)![]() .
.
(1)當(dāng)![]() 時(shí),求證:
時(shí),求證:![]() 在
在![]() 上是單調(diào)遞減函數(shù);
上是單調(diào)遞減函數(shù);
(2)若函數(shù)![]() 有兩個(gè)正零點(diǎn)
有兩個(gè)正零點(diǎn)![]() 、
、![]() ,求
,求![]() 的取值范圍,并證明:
的取值范圍,并證明:![]() .
.
【答案】(1)見(jiàn)證明;(2)實(shí)數(shù)![]() 的取值范圍是
的取值范圍是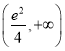 ,證明見(jiàn)解析.
,證明見(jiàn)解析.
【解析】
(1)由題意得出![]() 在區(qū)間
在區(qū)間![]() 上恒成立,由
上恒成立,由![]() 得出
得出![]()
![]() ,構(gòu)造函數(shù)
,構(gòu)造函數(shù)![]() ,證明
,證明![]() 在區(qū)間
在區(qū)間![]() 上恒成立即可;
上恒成立即可;
(2)由![]() 利用參變量分離法得出
利用參變量分離法得出![]() ,將題意轉(zhuǎn)化為當(dāng)直線(xiàn)
,將題意轉(zhuǎn)化為當(dāng)直線(xiàn)![]() 與函數(shù)
與函數(shù)![]() 在
在![]() 上有兩個(gè)交點(diǎn)時(shí)求
上有兩個(gè)交點(diǎn)時(shí)求![]() 的取值范圍,利用數(shù)形結(jié)合思想求解即可,然后由題意得出
的取值范圍,利用數(shù)形結(jié)合思想求解即可,然后由題意得出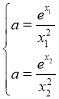 ,取自然對(duì)數(shù)得
,取自然對(duì)數(shù)得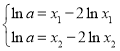 ,等式作差得
,等式作差得![]() ,利用分析得出所證不等式等價(jià)于
,利用分析得出所證不等式等價(jià)于![]() ,然后構(gòu)造函數(shù)
,然后構(gòu)造函數(shù)![]() 證明即可.
證明即可.
(1)![]() ,
,![]() .
.
由題意知,不等式![]() 在區(qū)間
在區(qū)間![]() 上恒成立,
上恒成立,
由于![]() ,當(dāng)
,當(dāng)![]() 時(shí),
時(shí),![]() ,
,
構(gòu)造函數(shù)![]() ,其中
,其中![]() ,則
,則![]() ,令
,令![]() ,得
,得![]() .
.
當(dāng)![]() 時(shí),
時(shí),![]() ;當(dāng)
;當(dāng)![]() 時(shí),
時(shí),![]() .
.
所以,函數(shù)![]() 在
在![]() 處取得極大值,亦即最大值,即
處取得極大值,亦即最大值,即![]() ,
,
![]() ,所以,
,所以,![]() .
.
所以,不等式![]() 在區(qū)間
在區(qū)間![]() 上恒成立,
上恒成立,
因此,當(dāng)![]() 時(shí),函數(shù)
時(shí),函數(shù)![]() 在
在![]() 上是單調(diào)遞減函數(shù);
上是單調(diào)遞減函數(shù);
(2)令![]() ,可得
,可得![]()
令![]() ,則
,則![]() .
.
當(dāng)![]() 時(shí),
時(shí),![]() ,當(dāng)
,當(dāng)![]() 時(shí),
時(shí),![]() .
.
當(dāng)![]() 時(shí),函數(shù)
時(shí),函數(shù)![]() 單調(diào)遞減,當(dāng)
單調(diào)遞減,當(dāng)![]() 時(shí),函數(shù)
時(shí),函數(shù)![]() 單調(diào)遞增.
單調(diào)遞增.
![]() ,
,
當(dāng)![]() 時(shí),
時(shí),![]() ,當(dāng)
,當(dāng)![]() 時(shí).
時(shí).![]() .
.
![]() 時(shí),函數(shù)
時(shí),函數(shù)![]() 有兩個(gè)正零點(diǎn),因此,實(shí)數(shù)
有兩個(gè)正零點(diǎn),因此,實(shí)數(shù)![]() 的取值范圍是
的取值范圍是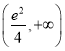 .
.
由上知![]() 時(shí),
時(shí),![]() ,
,
由題意得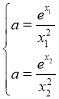 ,上述等式兩邊取自然對(duì)數(shù)得
,上述等式兩邊取自然對(duì)數(shù)得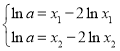 ,
,
兩式作差得![]() ,
,![]() ,
,
要證![]() ,即證
,即證![]() .
.
由于![]() ,則
,則![]() ,即證
,即證![]() ,
,
即證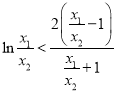 ,令
,令![]() ,即證
,即證![]() ,其中
,其中![]() .
.
構(gòu)造函數(shù)![]() ,其中
,其中![]() ,即證
,即證![]() 在
在![]() 上恒成立.
上恒成立.
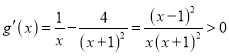 ,所以,函數(shù)
,所以,函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上恒成立,
上恒成立,
所以,![]() ,因此,
,因此,![]() .
.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】從集合![]() 的所有非空子集中,等可能地取出
的所有非空子集中,等可能地取出![]() 個(gè).
個(gè).
(1)若![]() ,求所取子集的元素既有奇數(shù)又有偶數(shù)的概率;
,求所取子集的元素既有奇數(shù)又有偶數(shù)的概率;
(2)若![]() ,記所取子集的元素個(gè)數(shù)之差為
,記所取子集的元素個(gè)數(shù)之差為![]() ,求
,求![]() 的分布列及數(shù)學(xué)期望
的分布列及數(shù)學(xué)期望![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】在國(guó)慶![]() 周年慶典活動(dòng)中,東城區(qū)教育系統(tǒng)近
周年慶典活動(dòng)中,東城區(qū)教育系統(tǒng)近![]() 名師生參與了國(guó)慶中心區(qū)合唱、
名師生參與了國(guó)慶中心區(qū)合唱、![]() 方陣群眾游行、聯(lián)歡晚會(huì)及
方陣群眾游行、聯(lián)歡晚會(huì)及![]() 萬(wàn)只氣球保障等多項(xiàng)重點(diǎn)任務(wù).設(shè)
萬(wàn)只氣球保障等多項(xiàng)重點(diǎn)任務(wù).設(shè)![]() 是參與國(guó)慶中心區(qū)合唱的學(xué)校
是參與國(guó)慶中心區(qū)合唱的學(xué)校![]() ,
,![]() 是參與27方陣群眾游行的學(xué)校
是參與27方陣群眾游行的學(xué)校![]() ,
,![]() 是參與國(guó)慶聯(lián)歡晚會(huì)的學(xué)校
是參與國(guó)慶聯(lián)歡晚會(huì)的學(xué)校![]() .請(qǐng)用上述集合之間的運(yùn)算來(lái)表示:①既參與國(guó)慶中心區(qū)合唱又參與27方陣群眾游行的學(xué)校的集合為_____;②至少參與國(guó)慶中心區(qū)合唱與國(guó)慶聯(lián)歡晚會(huì)中一項(xiàng)的學(xué)校的集合為_____.
.請(qǐng)用上述集合之間的運(yùn)算來(lái)表示:①既參與國(guó)慶中心區(qū)合唱又參與27方陣群眾游行的學(xué)校的集合為_____;②至少參與國(guó)慶中心區(qū)合唱與國(guó)慶聯(lián)歡晚會(huì)中一項(xiàng)的學(xué)校的集合為_____.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】定義在D上的函數(shù)f(x)如果滿(mǎn)足:對(duì)任意x∈D,存在常數(shù)M≥0,都有|f(x)|≤M成立,則稱(chēng)f(x)是D上的有界函數(shù),其中M稱(chēng)為函數(shù)f(x)的一個(gè)上界.已知函數(shù)![]() ,
,![]() .
.
(1)求函數(shù)f(x)在區(qū)間![]() 上的所有上界構(gòu)成的集合;
上的所有上界構(gòu)成的集合;
(2)若函數(shù)g(x)在[0,+∞)上是以7為上界的有界函數(shù),求實(shí)數(shù)a的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知復(fù)數(shù)z=![]() 2016+(1-i)2(其中i為虛數(shù)單位),若復(fù)數(shù)z的共軛復(fù)數(shù)為
2016+(1-i)2(其中i為虛數(shù)單位),若復(fù)數(shù)z的共軛復(fù)數(shù)為![]() ,且
,且![]() ·z1=4+3i.
·z1=4+3i.
(1)求復(fù)數(shù)z1;
(2)若z1是關(guān)于x的方程x2-px+q=0的一個(gè)根,求實(shí)數(shù)p,q的值,并求出方程x2-px+q=0的另一個(gè)復(fù)數(shù)根.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]() 的相鄰兩對(duì)稱(chēng)軸間的距離為
的相鄰兩對(duì)稱(chēng)軸間的距離為![]() ,若將
,若將![]() 的圖像先向左平移
的圖像先向左平移![]() 個(gè)單位,再向下平移
個(gè)單位,再向下平移![]() 個(gè)單位,所得的函數(shù)
個(gè)單位,所得的函數(shù)![]() 為奇函數(shù).
為奇函數(shù).
(1)求![]() 的解析式;
的解析式;
(2)若關(guān)于![]() 的方程
的方程![]() 在區(qū)間
在區(qū)間![]() 上有兩個(gè)不等實(shí)根,求實(shí)數(shù)
上有兩個(gè)不等實(shí)根,求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】(本小題滿(mǎn)分14分)某學(xué)校為了支持生物課程基地研究植物生長(zhǎng),計(jì)劃利用學(xué)校空地建造一間室內(nèi)面積為900m2的矩形溫室,在溫室內(nèi)劃出三塊全等的矩形區(qū)域,分別種植三種植物,相鄰矩形區(qū)域之間間隔1m,三塊矩形區(qū)域的前、后與內(nèi)墻各保留 1m 寬的通道,左、右兩塊矩形區(qū)域分別與相鄰的左右內(nèi)墻保留 3m 寬的通道,如圖.設(shè)矩形溫室的室內(nèi)長(zhǎng)為![]() (m),三塊種植植物的矩形區(qū)域的總面積為
(m),三塊種植植物的矩形區(qū)域的總面積為![]() (m2).
(m2).

(1)求![]() 關(guān)于
關(guān)于![]() 的函數(shù)關(guān)系式;
的函數(shù)關(guān)系式;
(2)求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】交通指數(shù)是交通擁堵指數(shù)的簡(jiǎn)稱(chēng),是綜合反映道路網(wǎng)暢通或擁堵的概念,記交通指數(shù)為![]() ,其范圍為
,其范圍為![]() ,分為五個(gè)級(jí)別,
,分為五個(gè)級(jí)別, ![]() 暢通;
暢通; ![]() 基本暢通;
基本暢通; ![]() 輕度擁堵;
輕度擁堵; ![]() 中度擁堵;
中度擁堵; ![]() 嚴(yán)重?fù)矶?早高峰時(shí)段(
嚴(yán)重?fù)矶?早高峰時(shí)段(![]() ),從某市交通指揮中心隨機(jī)選取了三環(huán)以?xún)?nèi)的50個(gè)交通路段,依據(jù)其交通指數(shù)數(shù)據(jù)繪制的頻率分布直方圖如圖.
),從某市交通指揮中心隨機(jī)選取了三環(huán)以?xún)?nèi)的50個(gè)交通路段,依據(jù)其交通指數(shù)數(shù)據(jù)繪制的頻率分布直方圖如圖.

(1)這50個(gè)路段為中度擁堵的有多少個(gè)?
(2)據(jù)此估計(jì),早高峰三環(huán)以?xún)?nèi)的三個(gè)路段至少有一個(gè)是嚴(yán)重?fù)矶碌母怕适嵌嗌伲?/span>
(3)某人上班路上所用時(shí)間若暢通時(shí)為20分鐘,基本暢通為30分鐘,輕度擁堵為36分鐘,中度擁堵為42分鐘,嚴(yán)重?fù)矶聻?0分鐘,求此人所用時(shí)間的數(shù)學(xué)期望.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】為慶祝黨的98歲生日,某高校組織了“歌頌祖國(guó),緊跟黨走”為主題的黨史知識(shí)競(jìng)賽。從參加競(jìng)賽的學(xué)生中,隨機(jī)抽取40名學(xué)生,將其成績(jī)分為六段![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,到如圖所示的頻率分布直方圖.
,到如圖所示的頻率分布直方圖.

(1)求圖中![]() 的值及樣本的中位數(shù)與眾數(shù);
的值及樣本的中位數(shù)與眾數(shù);
(2)若從競(jìng)賽成績(jī)?cè)?/span>![]() 與
與![]() 兩個(gè)分?jǐn)?shù)段的學(xué)生中隨機(jī)選取兩名學(xué)生,設(shè)這兩名學(xué)生的競(jìng)賽成績(jī)之差的絕對(duì)值不大于
兩個(gè)分?jǐn)?shù)段的學(xué)生中隨機(jī)選取兩名學(xué)生,設(shè)這兩名學(xué)生的競(jìng)賽成績(jī)之差的絕對(duì)值不大于![]() 分為事件
分為事件![]() ,求事件
,求事件![]() 發(fā)生的概率.
發(fā)生的概率.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com