【題目】已知函數(shù)
.
（1）當(dāng)
時，討論
的單調(diào)性；
（2）設(shè)
，若關(guān)于
的不等式
在
上有解，求
的取值范圍.
【答案】(1)見解析;(2) 
.
【解析】試題分析: （1）對函數(shù)兩次求導(dǎo),判斷出函數(shù)的單調(diào)性;(2)將函數(shù)g(x)的解析式代入關(guān)于x的不等式,化簡并構(gòu)造新函數(shù),對新函數(shù)求導(dǎo),討論參數(shù)的范圍判斷出單調(diào)性求出最值,代入不等式即可.
試題解析:
（1）由題意知， 
，
令
，當(dāng)
時， 
恒成立，
∴當(dāng)
時， 
；當(dāng)
時， 
，
∴函數(shù)
在
上單調(diào)遞增，在
上單調(diào)遞減.
（2）∵
，∴
，
由題意知，存在
，使得
成立.
即存在
，使得
成立，
令
，
∴
.
①
時， 
，則
，∴函數(shù)
在
上單調(diào)遞減，
∴
成立，解得
，∴
；
②當(dāng)
時，令
，解得
；令
，解得
，
∴函數(shù)
在
上單調(diào)遞增，在
上單調(diào)遞減，
又
，∴
，解得
，∴
無解；
③當(dāng)
時， 
，則
，∴函數(shù)
在
上單調(diào)遞增，
∴
，不符合題意，舍去；
綜上所述， 
的取值范圍為
.
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知四棱臺
的上下底面分別是邊長為2和4的正方形， 
= 4且 
⊥底面
，點
為
的中點．
(Ⅰ)求證： 
面 
;
(Ⅱ)在
邊上找一點
，使
∥面
，
并求三棱錐
的體積.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知甲盒子中有
個紅球，
個藍球，乙盒子中有
個紅球，
個藍球
，同時從甲乙兩個盒子中取出
個球進行交換，（a）交換后，從甲盒子中取1個球是紅球的概率記為
.（b）交換后，乙盒子中含有紅球的個數(shù)記為
.則（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】將函數(shù)
的圖象向左平移
個單位長度，再向上平移1個單位長度，得到函數(shù)
的圖象，則函數(shù)具有性質(zhì)__________．（填入所有正確性質(zhì)的序號）
①最大值為
，圖象關(guān)于直線
對稱；
②圖象關(guān)于
軸對稱；
③最小正周期為
；
④圖象關(guān)于點
對稱；
⑤在
上單調(diào)遞減
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知函數(shù)f（x）＝xlnx
x2﹣ax+1．
（1）設(shè)g（x）＝f′（x），求g（x）的單調(diào)區(qū)間；
（2）若f（x）有兩個極值點x1，x2，求證：x1+x2＞2．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】王老師的班上有四個體育健將甲、乙、丙、丁，他們都特別擅長短跑，在某次運動會上，他們四人要組成一個
米接力隊，王老師要安排他們四個人的出場順序，以下是他們四人的對話：
甲：我不跑第一棒和第二棒；乙：我不跑第一棒和第四棒；
丙：我也不跑第一棒和第四棒；丁：如果乙不跑第二棒，我就不跑第一棒；
王老師聽了他們四人的對話，安排了一種合理的出場順序，滿足了他們的所有要求， 據(jù)此我們可以斷定，在王老師安排的出場順序中，跑第三棒的人是（ ）
A. 甲 B. 乙 C. 丙 D. 丁
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
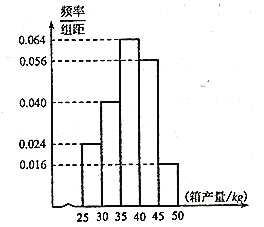
【題目】海水養(yǎng)殖場使用網(wǎng)箱養(yǎng)殖的方法，收獲時隨機抽取了 100個網(wǎng)箱，測量各箱水產(chǎn)品的產(chǎn)量(單位:
)，其頻率分布直方圖如圖：
定義箱產(chǎn)量在
(單位:)的網(wǎng)箱為“穩(wěn)產(chǎn)網(wǎng)箱”， 箱產(chǎn)量在區(qū)間之外的網(wǎng)箱為“非穩(wěn)產(chǎn)網(wǎng)箱”.
（1）從該養(yǎng)殖場（該養(yǎng)殖場中的網(wǎng)箱數(shù)量是巨大的）中隨機抽取3個網(wǎng)箱.將頻率視為概率，設(shè)其中穩(wěn)產(chǎn)網(wǎng)箱的個數(shù)為
，求的分布列與期望
；
（2）從樣本中隨機抽取3個網(wǎng)箱，設(shè)其中穩(wěn)產(chǎn)網(wǎng)箱的個數(shù)為
，試比較的期望
與的大小.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】定義在
上的函數(shù)
，若已知其在
內(nèi)只取到一個最大值和一個最小值，且當(dāng)
時函數(shù)取得最大值為
；當(dāng)
，函數(shù)取得最小值為
．
（1）求出此函數(shù)的解析式；
（2）若將函數(shù)
的圖像保持橫坐標(biāo)不變縱坐標(biāo)變?yōu)樵瓉淼?/span>
得到函數(shù)
，再將函數(shù)的圖像向左平移
個單位得到函數(shù)
，已知函數(shù)
的最大值為
，求滿足條件的
的最小值；
（3）是否存在實數(shù)
，滿足不等式
？若存在，求出的范圍（或值），若不存在，請說明理由．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知函數(shù)
（1）試討論
在
極值點的個數(shù)；
（2）若函數(shù)
的兩個極值點為
，且
，
為
的導(dǎo)函數(shù)，設(shè)
，求實數(shù)
的取值范圍．
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com