【題目】已知等差數列{an}的公差d＞0，其前n項和為Sn ， 若S3=12，且2a1 ， a2 ， 1+a3成等比數列．
（1）求數列{an}的通項公式；
（2）記bn= 
（n∈N*），且數列{bn}的前n項和為Tn ， 證明： 
≤Tn＜ ．
【答案】
（1）解：依題意，得 
，
即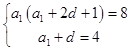 
，得d2+d﹣12=0．
∵d＞0，∴d=3，a1=1．
∴數列{an}的通項公式an=1+3（n﹣1）=3n﹣2
（2）證明：∵ 
，
前n項和為Tn= 
（1﹣ + ﹣ 
+…+ 
﹣ 
）
= ×（1﹣ ）= 
，
由Tn遞增，可得Tn≥T1= ，
又Tn＜ ，則 
【解析】（1）由等差數列的通項公式和等比數列的性質，解方程可得首項和公差，即可得到所求通項公式；（2）求得bn= （ ﹣ ），再由數列的求和方法：裂項相消求和，結合數列的單調性和不等式的性質，即可得證．
【考點精析】掌握數列的前n項和是解答本題的根本，需要知道數列{an}的前n項和sn與通項an的關系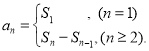
．
科目：高中數學 來源： 題型：
【題目】已知函數
（1）若曲線
在點
處的切線與直線
垂直，求函數的極值；
（2）設函數
.當
=
時，若區間[1，e]上存在x0，使得
，求實數
的取值范圍．（
為自然對數底數）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】給出下列結論：①y=1是冪函數；
②定義在R上的奇函數y=f（x）滿足f（0）=0
③函數 
是奇函數
④當a＜0時， 
⑤函數y=1的零點有2個；
其中正確結論的序號是（寫出所有正確結論的編號）．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）=x2+3x+a
（1）當a=﹣2時，求不等式f（x）＞2的解集
（2）若對任意的x∈[1，+∞），f（x）＞0恒成立，求實數a的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知點P（a，b）（ab≠0）是圓x2+y2=r2內的一點，直線m是以P為中點的弦所在直線，直線l的方程為ax+by=r2 ， 那么（ ）
A.m∥l，且l與圓相交
B.m⊥l，且l與圓相切
C.m∥l，且l與圓相離
D.m⊥l，且l與圓相離
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）=x2﹣2ax+5（a＞1），
（1）若f（x）的定義域和值域均是[1，a]，求實數a的值；
（2）若f（x）在區間（﹣∞，2]上是減函數，且對任意的x∈[1，a+1]，都有f（x）≤0，求實數a的取值范圍；
（3）若g（x）=2x+log2（x+1），且對任意的x∈[0，1]，都存在x0∈[0，1]，使得f（x0）=g（x）成立，求實數a的取值范圍．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
