
已知函數 .
.
(Ⅰ)若函數在區(qū)間 上存在極值,求實數
上存在極值,求實數 的取值范圍;
的取值范圍;
(Ⅱ)如果當 時,不等式
時,不等式 恒成立,求實數
恒成立,求實數 的取值范圍,并且判斷代數式
的取值范圍,并且判斷代數式 的大小.
的大小.
(Ⅰ)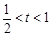 ;(Ⅱ)
;(Ⅱ)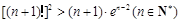
解析試題分析:(Ⅰ)先對函數求導,求出函數的極值,根據函數 在區(qū)間
在區(qū)間 上存在極值,
上存在極值,
所以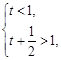 從而解得
從而解得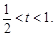 (Ⅱ)不等式
(Ⅱ)不等式 恒成立問題轉化為求函數的最值問題,根據不等式的性質比較
恒成立問題轉化為求函數的最值問題,根據不等式的性質比較 的大小.
的大小.
試題解析:
解:(Ⅰ)因為 ,
,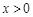 ,則
,則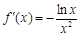 , (1分)
, (1分)
當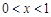 時,
時,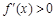 ;當
;當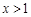 時,
時,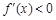 .
.
所以 在
在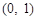 上單調遞增;在
上單調遞增;在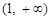 上單調遞減,
上單調遞減,
所以函數 在
在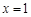 處取得極大值. (2分)
處取得極大值. (2分)
因為函數 在區(qū)間
在區(qū)間 上存在極值,
上存在極值,
所以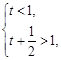 解得
解得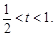 (4分)
(4分)
(Ⅱ)不等式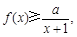 即為
即為 記
記 ,
,
所以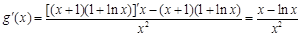 . (5分)
. (5分)
令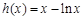 ,則
,則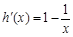 ,
,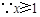 ,
,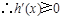 ,
,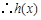 在
在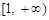 上單調遞增,
上單調遞增, ,從而
,從而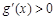 ,
,
故 在
在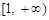 上也單調遞增,所以
上也單調遞增,所以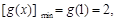
所以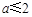 . (7分)
. (7分)
由上述知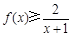 恒成立,即
恒成立,即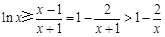 ,
,
令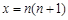 ,則
,則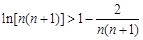 ,
,
∴  ,
, ,
,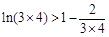 , ,
, ,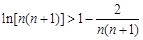 , (9分)
, (9分)
疊加得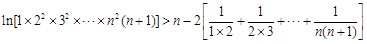
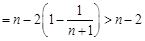 .
.
則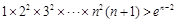 ,
,
所以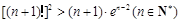 . (12分)
. (12分)
考點:函數與導數,函數極值與最值,不等式恒成立問題,不等式的性質.


 開心快樂假期作業(yè)暑假作業(yè)西安出版社系列答案
開心快樂假期作業(yè)暑假作業(yè)西安出版社系列答案科目:高中數學 來源: 題型:解答題
(理)已知函數f(x)=  -lnx,x∈[1,3].
-lnx,x∈[1,3].
(Ⅰ)求f(x)的最大值與最小值;
(Ⅱ)若f(x)<4-At對于任意的x∈[1,3],t∈[0,2]恒成立,求實數A的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知函數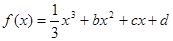 ,設曲線
,設曲線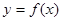 在與
在與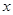 軸交點處的切線為
軸交點處的切線為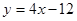 ,
,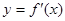 為
為 的導函數,滿足
的導函數,滿足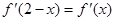 .
.
(1)求 ;
;
(2)設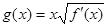 ,
,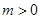 ,求函數
,求函數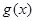 在
在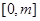 上的最大值;
上的最大值;
(3)設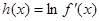 ,若對于一切
,若對于一切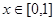 ,不等式
,不等式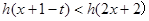 恒成立,求實數
恒成立,求實數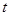 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
設函數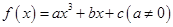 為奇函數,其圖象在點
為奇函數,其圖象在點 處的切線與直線
處的切線與直線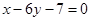 垂直,導函數
垂直,導函數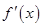 的最小值為
的最小值為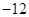 .
.
(1)求 的值;
的值;
(2)求函數 的單調遞增區(qū)間,并求函數
的單調遞增區(qū)間,并求函數 在
在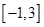 上的最大值和最小值.
上的最大值和最小值.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com