Question

【題目】如圖，AB是圓O的直徑，C是圓O上不同于A，B的一點，PA⊥平面ABC，E是PC的中點，，PA=AC=1．

（1）求證：AE⊥PB;

（2）求三棱錐C-ABE的體積.

（3）求二面角A-PB-C的正弦值．

Answer 1

【答案】（1）詳見解析；（2）；（3）.

【解析】

（1）由線面垂直得PA⊥BC，由圓O的直徑，得AC⊥BC，從而AE平面PAC，進而BC⊥AE，由等腰三角形性質得AE⊥PC，由此能證明AE⊥PB．

（2）求，轉化為以E為頂點，以ABC為底面時的體積來求即可。

（3）過A作AF⊥PB交PB于F，連接EF，推導出∠AFE是二面角APBC的平面角，由此能求出二面角APBC的正弦值．

解：（1）證明：∵PA⊥平面ABC，BC平面ABC

∴PA⊥BC，

又AB是圓O的直徑，C是圓O上不同于A，B的一點

∴∠ACB＝90°，即AC⊥BC，又PA∩AC＝A

∴BC⊥平面PAC，又AE平面PAC

∴BC⊥AE

∵PA＝AC，E是PC的中點

∴AE⊥PC，又BC∩PC＝C

∴AE⊥平面PBC，又PB平面PBC

∴AE⊥PB．

（2）由已知可得

對于以E為頂點，以為底面時，

因為E是PC的中點，所以E到面ABC的距離等于，

在中，

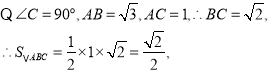
（3）過A作AF⊥PB交PB于F，連接EF

又由（1）得AE⊥PB，AE∩AF＝A

∴PB⊥平面AEF，又EF平面AEF

∴PB⊥EF，又AF⊥PB

∴∠AFE是二面角APBC的平面角

∵在Rt△PAC中，PA＝AC＝1，則

在Rt△PAB中，PA＝1，AB＝，同理得

∴在Rt△AEF中，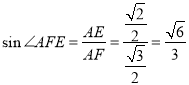

故二面角APBC的正弦值為