
【題目】已知函數(shù)f(x)=x3-3x2+1,g(x)= ,若方程g[f(x)]-a=0(a>0)有6個實(shí)數(shù)根(互不相同),則實(shí)數(shù)a的取值范圍是______.
,若方程g[f(x)]-a=0(a>0)有6個實(shí)數(shù)根(互不相同),則實(shí)數(shù)a的取值范圍是______.
【答案】![]()
【解析】分析:利用換元法設(shè)t=f(x),則g(t)=a分別作出兩個函數(shù)的圖象,根據(jù)a的取值確定t的取值范圍,利用數(shù)形結(jié)合進(jìn)行求解判斷即可.
詳解:作出函數(shù)f(x)和g(x)的圖象如圖: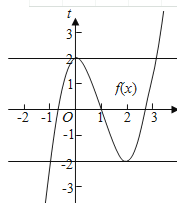 ,
,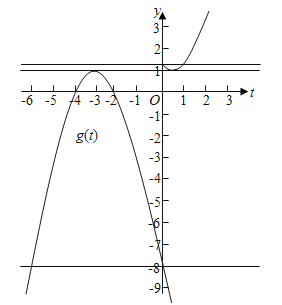 ,由g[f(x)]-a=0(a>0)得g[f(x)]=a,(a>0)設(shè)t=f(x),則g(t)=a,(a>0)由y=g(t)的圖象知,①當(dāng)0<a<1時,方程g(t)=a有兩個根-4<t1<-3,或-4<t2<-2,由t=f(x)的圖象知,當(dāng)-4<t1<-3時,t=f(x)有0個根,當(dāng)-4<t2<-2時,t=f(x)有0個根,此時方程g[f(x)]-a=0(a>0)有0個根,②當(dāng)a=1時,方程g(t)=a有兩個根t1=-3,或t2=
,由g[f(x)]-a=0(a>0)得g[f(x)]=a,(a>0)設(shè)t=f(x),則g(t)=a,(a>0)由y=g(t)的圖象知,①當(dāng)0<a<1時,方程g(t)=a有兩個根-4<t1<-3,或-4<t2<-2,由t=f(x)的圖象知,當(dāng)-4<t1<-3時,t=f(x)有0個根,當(dāng)-4<t2<-2時,t=f(x)有0個根,此時方程g[f(x)]-a=0(a>0)有0個根,②當(dāng)a=1時,方程g(t)=a有兩個根t1=-3,或t2=![]() ,由t=f(x)的圖象知,當(dāng)t1=-3時,t=f(x)有0個根,當(dāng)t2=
,由t=f(x)的圖象知,當(dāng)t1=-3時,t=f(x)有0個根,當(dāng)t2=![]() 時,t=f(x)有3個根,此時方程g[f(x)]-a=0(a>0)有3個根,③當(dāng)1<a<
時,t=f(x)有3個根,此時方程g[f(x)]-a=0(a>0)有3個根,③當(dāng)1<a<![]() 時,方程g(t)=a有兩個根0<t1<
時,方程g(t)=a有兩個根0<t1<![]() ,或
,或![]() <t2<1,由t=f(x)的圖象知,當(dāng)0<t1<
<t2<1,由t=f(x)的圖象知,當(dāng)0<t1<![]() 時,t=f(x)有3個根,當(dāng)
時,t=f(x)有3個根,當(dāng)![]() <t2<1時,t=f(x)有3個根,此時方程g[f(x)]-a=0(a>0)有3+3=6個根,當(dāng)a=
<t2<1時,t=f(x)有3個根,此時方程g[f(x)]-a=0(a>0)有3+3=6個根,當(dāng)a=![]() 由圖可得同理只有5解,綜合的故若方程g[f(x)]-a=0(a>0)有6個實(shí)數(shù)根(互不相同),則實(shí)數(shù)a的取值范圍是
由圖可得同理只有5解,綜合的故若方程g[f(x)]-a=0(a>0)有6個實(shí)數(shù)根(互不相同),則實(shí)數(shù)a的取值范圍是![]()



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】公元263年左右,我國數(shù)學(xué)家劉徽發(fā)現(xiàn)當(dāng)圓內(nèi)接正多邊形的邊數(shù)無限增加時,多邊形面積可無限逼近圓的面積,并創(chuàng)立了“割圓術(shù)”,利用“割圓術(shù)”劉徽得到了圓周率精確到小數(shù)點(diǎn)后兩位的近似值3.14,這就是著名的“徽率”.如圖是利用劉徽的“割圓術(shù)”思想設(shè)計(jì)的一個程序框圖,則輸出n的值為( )(參考數(shù)據(jù):sin15°=0.2588,sin7.5°=0.1305)

A. 12B. 24C. 48D. 96
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】下圖是某地區(qū)2000年至2016年環(huán)境基礎(chǔ)設(shè)施投資額![]() (單位:億元)的折線圖.
(單位:億元)的折線圖.
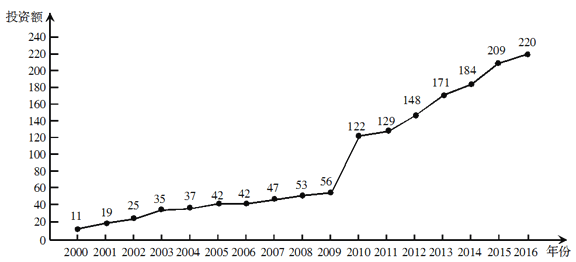
為了預(yù)測該地區(qū)2018年的環(huán)境基礎(chǔ)設(shè)施投資額,建立了![]() 與時間變量
與時間變量![]() 的兩個線性回歸模型.根據(jù)2000年至2016年的數(shù)據(jù)(時間變量
的兩個線性回歸模型.根據(jù)2000年至2016年的數(shù)據(jù)(時間變量![]() 的值依次為
的值依次為![]() )建立模型①:
)建立模型①:![]() ;根據(jù)2010年至2016年的數(shù)據(jù)(時間變量
;根據(jù)2010年至2016年的數(shù)據(jù)(時間變量![]() 的值依次為
的值依次為![]() )建立模型②:
)建立模型②:![]() .
.
(1)分別利用這兩個模型,求該地區(qū)2018年的環(huán)境基礎(chǔ)設(shè)施投資額的預(yù)測值;
(2)你認(rèn)為用哪個模型得到的預(yù)測值更可靠?并說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,某種水箱用的“浮球”,是由兩個半球和一個圓柱筒組成的.已知半球的直徑是6 cm,圓柱筒高為2 cm.

(1)這種“浮球”的體積是多少cm3(結(jié)果精確到0.1)?
(2)要在2 500個這樣的“浮球”表面涂一層膠,如果每平方米需要涂膠100克,那么共需膠多少克?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某種新產(chǎn)品投放市場的100天中,前40天價格呈直線上升,而后60天其價格呈直線下降,現(xiàn)統(tǒng)計(jì)出其中4天的價格如下表:
時間 | 第4天 | 第32天 | 第60天 | 第90天 |
價格(千元) | 23 | 30 | 22 | 7 |
(1)寫出價格![]() 關(guān)于時間
關(guān)于時間![]() 的函數(shù)關(guān)系式;(
的函數(shù)關(guān)系式;(![]() 表示投放市場的第
表示投放市場的第![]() 天);
天);
(2)銷售量![]() 與時間
與時間![]() 的函數(shù)關(guān)系:
的函數(shù)關(guān)系:![]() ,則該產(chǎn)品投放市場第幾天銷售額最高?最高為多少千元?
,則該產(chǎn)品投放市場第幾天銷售額最高?最高為多少千元?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() ,
,![]() .用
.用![]() 表示m,n中的最小值,設(shè)函數(shù)
表示m,n中的最小值,設(shè)函數(shù)![]() .
.
(1)當(dāng)![]() 時,求
時,求![]() 的最大值;
的最大值;
(2)討論![]() 零點(diǎn)的個數(shù).
零點(diǎn)的個數(shù).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,![]() 三個警亭有直道相通,已知
三個警亭有直道相通,已知![]() 在
在![]() 的正北方向6千米處,
的正北方向6千米處,![]() 在
在![]() 的正東方向
的正東方向![]() 千米處.
千米處.
(1)警員甲從![]() 出發(fā),沿
出發(fā),沿![]() 行至點(diǎn)
行至點(diǎn)![]() 處,此時
處,此時![]() ,求
,求![]() 的距離;
的距離;
(2)警員甲從![]() 出發(fā)沿
出發(fā)沿![]() 前往
前往![]() ,警員乙從
,警員乙從![]() 出發(fā)沿
出發(fā)沿![]() 前往
前往![]() ,兩人同時出發(fā),甲的速度為3千米/小時,乙的速度為6千米/小時.兩人通過專用對講機(jī)保持聯(lián)系,乙到達(dá)
,兩人同時出發(fā),甲的速度為3千米/小時,乙的速度為6千米/小時.兩人通過專用對講機(jī)保持聯(lián)系,乙到達(dá)![]() 后原地等待,直到甲到達(dá)
后原地等待,直到甲到達(dá)![]() 時任務(wù)結(jié)束.若對講機(jī)的有效通話距離不超過9千米,試問兩人通過對講機(jī)能保持聯(lián)系的總時長?
時任務(wù)結(jié)束.若對講機(jī)的有效通話距離不超過9千米,試問兩人通過對講機(jī)能保持聯(lián)系的總時長?

查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知拋物線![]() 的焦點(diǎn)為
的焦點(diǎn)為![]() ,
,![]() 是
是![]() 上一點(diǎn),且
上一點(diǎn),且![]() .
.
(1)求![]() 的方程;
的方程;
(2)設(shè)點(diǎn)![]() 是
是![]() 上異于點(diǎn)
上異于點(diǎn)![]() 的一點(diǎn),直線
的一點(diǎn),直線![]() 與直線
與直線![]() 交于點(diǎn)
交于點(diǎn)![]() ,過點(diǎn)
,過點(diǎn)![]() 作
作![]() 軸的垂線交
軸的垂線交![]() 于點(diǎn)
于點(diǎn)![]() ,證明:直線
,證明:直線![]() 過定點(diǎn).
過定點(diǎn).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() 的圖象與
的圖象與![]() 軸的交點(diǎn)中,相鄰兩個交點(diǎn)之間的距離為
軸的交點(diǎn)中,相鄰兩個交點(diǎn)之間的距離為![]() ,且圖象過點(diǎn)
,且圖象過點(diǎn)![]()
(1)求![]() 的解析式;
的解析式;
(2)求函數(shù)![]() 的單調(diào)遞增區(qū)間;
的單調(diào)遞增區(qū)間;
(3)將函數(shù)![]() 的圖象向右平移
的圖象向右平移![]() 個單位,再將圖象上各點(diǎn)的橫坐標(biāo)伸長到原來的2倍(縱坐標(biāo)不變),得到函數(shù)
個單位,再將圖象上各點(diǎn)的橫坐標(biāo)伸長到原來的2倍(縱坐標(biāo)不變),得到函數(shù)![]() 的圖象,若關(guān)于
的圖象,若關(guān)于![]() 的方程
的方程![]() ,在區(qū)間
,在區(qū)間![]() 上有且只有一個實(shí)數(shù)解,求實(shí)數(shù)
上有且只有一個實(shí)數(shù)解,求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com