【題目】【選修4-4，坐標(biāo)系與參數(shù)方程】
在直角坐標(biāo)系
中，直線
的參數(shù)方程為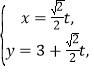
（t為參數(shù)），在以O為極點，
軸正半軸為極軸的極坐標(biāo)系中，曲線C的極坐標(biāo)方程為
（Ⅰ）求直線的普通方程與曲線C的直角坐標(biāo)方程；
（Ⅱ）若直線與
軸的交點為P，直線與曲線C的交點為A,B,求
的值.
【答案】（1）直線
的普通方程為
，曲線
的直角坐標(biāo)方程為
；（2）
．
【解析】試題本題主要考查參數(shù)方程、極坐標(biāo)方程與直角坐標(biāo)方程的轉(zhuǎn)化、直線與圓的位置關(guān)系等基礎(chǔ)知識，考查學(xué)生的分析問題解決問題的能力、轉(zhuǎn)化能力、計算能力. 第一問，利用
，
，
轉(zhuǎn)化方程；第二問，將直線方程與曲線方程聯(lián)立，消參，得到關(guān)于
的方程，利用兩根之積得到結(jié)論.
試題解析：（Ⅰ）直線的普通方程為，
，
曲線的直角坐標(biāo)方程為.
（Ⅱ）將直線的參數(shù)方程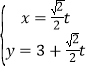
（為參數(shù)）代入曲線：，得到：
，
，
.
天天向上一本好卷系列答案
小學(xué)生10分鐘應(yīng)用題系列答案科目：高中數(shù)學(xué) 來源： 題型：
【題目】如圖，四棱錐
的底面
是直角梯形,
,
,側(cè)面
底面,
是等邊三角形，
，點
分別是棱
的中點 .
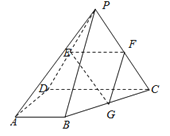
（Ⅰ）求證：
平面
；
（Ⅱ）求二面角
的大小；
（Ⅲ）在線段
上存在一點
，使
平面
，且
，求
的值.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】[選修4—4：坐標(biāo)系與參數(shù)方程]
在直角坐標(biāo)系
中，曲線
的方程為
．以坐標(biāo)原點為極點，
軸正半軸為極軸建立極坐標(biāo)系，曲線
的極坐標(biāo)方程為
．
（1）求的直角坐標(biāo)方程；
（2）若與有且僅有三個公共點，求的方程．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】在位于城市A南偏西
相距100海里的B處，一股臺風(fēng)沿著正東方向襲來，風(fēng)速為120海里/小時，臺風(fēng)影響的半徑為
海里
（1）若
，求臺風(fēng)影響城市A持續(xù)的時間（精確到1分鐘）？
（2）若臺風(fēng)影響城市A持續(xù)的時間不超過1小時，求
的取值范圍
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】在直角坐標(biāo)系
中，已知定點
、
，動點
滿足
，設(shè)點的曲線為
，直線
與交于
兩點.
（1）寫出曲線的方程，并指出曲線的軌跡；
（2）當(dāng)
，求實數(shù)
的取值范圍；
（3）證明：存在直線
，滿足
，并求實數(shù)
的取值范圍.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知
，（其中常數(shù)
）.
（1）當(dāng)
時，求函數(shù)
的極值；
（2）若函數(shù)
有兩個零點
，求證：
.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】在平面直角坐標(biāo)系xoy中，以坐標(biāo)原點O為極點，x軸正半軸為極軸建立極坐標(biāo)系。已知曲線C的極坐標(biāo)方程為
，過點
的直線l的參數(shù)方程為
（為參數(shù)），直線l與曲線C交于M、N兩點。
（1）寫出直線l的普通方程和曲線C的直角坐標(biāo)方程：
（2）若
成等比數(shù)列，求a的值。
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】動圓
與
相外切，與
相內(nèi)切．
（1）求動圓圓心的軌跡
的方程；
（2）
是動圓的半徑最小時的圓，傾斜角為
且過點
的直線l與相切，與軌跡交于
，
兩點，求
的值．
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
