
【題目】已知函數(shù)f(x)=aex﹣x(a∈R),其中e為自然對數(shù)的底數(shù),e=2.71828…
(Ⅰ)判斷函數(shù)f(x)的單調(diào)性,并說明理由
(Ⅱ)若x∈[1,2],不等式f(x)≥e﹣x恒成立,求a的取值范圍.
【答案】解:(Ⅰ)由f(x)=aex﹣x,得f′(x)=aex﹣1, 當(dāng)a≤0時,f′(x)<0,f(x)=aex﹣x為R上的減函數(shù);
當(dāng)a>0時,令aex﹣1=0,得x=lna,
若x∈(﹣∞,﹣lna),則f′(x)<0,此時f(x)為的單調(diào)減函數(shù);
若x∈(﹣lna,+∞),則f′(x)>0,此時f(x)為的單調(diào)增函數(shù).
綜上所述,當(dāng)a≤0時,f(x)=aex﹣x為R上的減函數(shù);
當(dāng)a>0時,若x∈(﹣∞,﹣lna),f(x)為的單調(diào)減函數(shù);
若x∈(﹣lna,+∞),f(x)為的單調(diào)增函數(shù).
(Ⅱ)由題意,x∈[1,2],不等式f(x)≥e﹣x恒成立,等價于aex﹣x≥e﹣x恒成立,
即x∈[1,2], ![]() 恒成立.
恒成立.
令g(x)= ![]() ,則問題等價于a不小于函數(shù)g(x)在[1,2]上的最大值.
,則問題等價于a不小于函數(shù)g(x)在[1,2]上的最大值.
由g(x)= ![]() =
= ![]() ,函數(shù)y=
,函數(shù)y= ![]() 在[1,2]上單調(diào)遞減,
在[1,2]上單調(diào)遞減,
令h(x)= ![]() ,x∈[1,2],h′(x)=
,x∈[1,2],h′(x)= ![]() .
.
∴h(x)= ![]() 在x∈[1,2]上也是減函數(shù),
在x∈[1,2]上也是減函數(shù),
∴g(x)在x∈[1,2]上也是減函數(shù),
∴g(x)在[1,2]上的最大值為g(1)= ![]() .
.
故x∈[1,2],不等式f(x)≥e﹣x恒成立的實(shí)數(shù)a的取值范圍是[ ![]() ,+∞).
,+∞).
【解析】(Ⅰ)求出原函數(shù)的導(dǎo)函數(shù),然后對a分類,當(dāng)a≤0時,f′(x)<0,f(x)=aex﹣x為R上的減函數(shù);當(dāng)a>0時,由導(dǎo)函數(shù)為0求得導(dǎo)函數(shù)的零點(diǎn),再由導(dǎo)函數(shù)的零點(diǎn)對定義域分段,根據(jù)導(dǎo)函數(shù)在各區(qū)間段內(nèi)的符號得到原函數(shù)的單調(diào)性;(Ⅱ)x∈[1,2],不等式f(x)≥e﹣x恒成立,等價于aex﹣x≥e﹣x恒成立,分離參數(shù)a,可得 ![]() 恒成立.令g(x)=
恒成立.令g(x)= ![]() ,則問題等價于a不小于函數(shù)g(x)在[1,2]上的最大值,然后利用導(dǎo)數(shù)求得函數(shù)g(x)在[1,2]上的最大值得答案.
,則問題等價于a不小于函數(shù)g(x)在[1,2]上的最大值,然后利用導(dǎo)數(shù)求得函數(shù)g(x)在[1,2]上的最大值得答案.
【考點(diǎn)精析】解答此題的關(guān)鍵在于理解函數(shù)單調(diào)性的判斷方法的相關(guān)知識,掌握單調(diào)性的判定法:①設(shè)x1,x2是所研究區(qū)間內(nèi)任兩個自變量,且x1<x2;②判定f(x1)與f(x2)的大小;③作差比較或作商比較.


 名校通行證有效作業(yè)系列答案
名校通行證有效作業(yè)系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】2017年春晚分會場之一是涼山西昌,電視播出后,通過網(wǎng)絡(luò)對涼山分會場的表演進(jìn)行了調(diào)查.調(diào)查分三類人群進(jìn)行,參加了網(wǎng)絡(luò)調(diào)查的觀眾們的看法情況如下:
觀眾對涼山分會場表演的看法 | 非常好 | 好 |
中國人且非四川(人數(shù)比例) |
|
|
四川人(非涼山)(人數(shù)比例) |
|
|
涼山人(人數(shù)比例) |
|
|
(1)從這三類人群中各選一個人,求恰好有2人認(rèn)為“非常好”的概率(用比例作為相應(yīng)概率);
(2)若在四川人(非涼山)群中按所持態(tài)度分層抽樣,抽取9人,在這9人中任意選取3人,認(rèn)為“非常好”的人數(shù)記為ξ,求ξ的分布列和數(shù)學(xué)期望.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某公司計劃購買1臺機(jī)器,該種機(jī)器使用三年后即被淘汰.機(jī)器有一易損零件,在購進(jìn)機(jī)器時,可以額外購買這種零件作為備件,每個200元. 在機(jī)器使用期間,如果備件不足再購買,則每個500元.現(xiàn)需決策在購買機(jī)器時應(yīng)同時購買幾個易損零件,為此搜集并整理了100臺這種機(jī)器在三年使用期內(nèi)更換的易損零件數(shù),得下面柱狀圖:

記x表示1臺機(jī)器在三年使用期內(nèi)需更換的易損零件數(shù),y表示1臺機(jī)器在購買易損零件上所需的費(fèi)用(單位:元),![]() 表示購機(jī)的同時購買的易損零件數(shù).
表示購機(jī)的同時購買的易損零件數(shù).
(1)若![]() =19,求y與x的函數(shù)解析式;
=19,求y與x的函數(shù)解析式;
(2)若要求“需更換的易損零件數(shù)不大于![]() ”的頻率不小于0.8,求
”的頻率不小于0.8,求![]() 的最小值;
的最小值;
(3)假設(shè)這100臺機(jī)器在購機(jī)的同時每臺都購買18個易損零件,或每臺都購買19個易損零件,分別計算這100臺機(jī)器在購買易損零件上所需費(fèi)用的平均數(shù),以此作為決策依據(jù),購買1臺機(jī)器的同時應(yīng)購買18個還是19個易損零件?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知△ABC的內(nèi)角A,B,C的對邊分別為a,b,c,2acosC=bcosC+ccosB.
(1)求角C的大小;
(2)若c=![]() ,a2+b2=10,求△ABC的面積.
,a2+b2=10,求△ABC的面積.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】張三同學(xué)從7歲起到13歲每年生日時對自己的身高測量后記錄如表:
年齡 (歲) | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
身高 (cm) | 121 | 128 | 135 | 141 | 148 | 154 | 160 |
(Ⅰ)求身高y關(guān)于年齡x的線性回歸方程;
(Ⅱ)利用(Ⅰ)中的線性回歸方程,分析張三同學(xué)7歲至13歲身高的變化情況,如17歲之前都符合這一變化,請預(yù)測張三同學(xué)15歲時的身高.
附:回歸直線的斜率和截距的最小二乘法估計公式分別為:![]() =
= 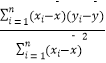 ,
, ![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)數(shù)列{an}的前n項(xiàng)和Sn滿足:Sn=nan﹣2n(n﹣1),首項(xiàng)![]() =1.
=1.
(1)求數(shù)列{an}的通項(xiàng)公式;
(2)設(shè)數(shù)列![]() 的前n項(xiàng)和為Mn,求證:
的前n項(xiàng)和為Mn,求證:![]()
![]() Mn
Mn![]()
![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)![]() 分別為雙曲線
分別為雙曲線![]() 的左、右頂點(diǎn),雙曲線的實(shí)軸長為
的左、右頂點(diǎn),雙曲線的實(shí)軸長為![]() ,焦點(diǎn)到漸近線的距離為
,焦點(diǎn)到漸近線的距離為![]() .
.
(1)求雙曲線的方程;
(2)已知直線![]() 與雙曲線的右支交于
與雙曲線的右支交于![]() 兩點(diǎn),且在雙曲線的右支上存在點(diǎn)
兩點(diǎn),且在雙曲線的右支上存在點(diǎn)![]() ,使
,使![]() ,求
,求![]() 的值及點(diǎn)
的值及點(diǎn)![]() 的坐標(biāo).
的坐標(biāo).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)f(x)=sinωx+cosωx(ω>0),x∈R,若函數(shù)f(x)在區(qū)間(﹣ω,ω)內(nèi)單調(diào)遞增,且函數(shù)y=f(x)的圖象關(guān)于直線x=ω對稱,則ω的值為 .
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知點(diǎn)![]() ,
,![]() ,直線
,直線![]() 與直線
與直線![]() 相交于點(diǎn)
相交于點(diǎn)![]() ,直線
,直線![]() 與直線
與直線![]() 的斜率分別記為
的斜率分別記為![]() 與
與![]() ,且
,且![]() .
.
(1)求點(diǎn)![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(2)過定點(diǎn)![]() 作直線
作直線![]() 與曲線
與曲線![]() 交于
交于![]() 兩點(diǎn),
兩點(diǎn), ![]() 的面積是否存在最大值?若存在,求出
的面積是否存在最大值?若存在,求出![]() 面積的最大值;若不存在,請說明理由.
面積的最大值;若不存在,請說明理由.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com