
【題目】已知![]() 是公差不為零的等差數列,
是公差不為零的等差數列,![]() 且
且![]() 成等比數列.
成等比數列.
(1)求數列![]() 的通項公式;
的通項公式;
(2)求數列![]() 的前
的前![]() 項和
項和![]() .
.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】試題分析:(1)設數列![]() 的公差為
的公差為![]() ,由
,由![]() ,且
,且![]() 成等比數列,可得
成等比數列,可得![]() ,即
,即![]() ,解出
,解出![]() 即可得出通項公式;(2)根據等比數列和等差數列的前
即可得出通項公式;(2)根據等比數列和等差數列的前![]() 項和公式,分組求和即可.
項和公式,分組求和即可.
試題解析:(1):設數列{an}的公差為d≠0.∵a1=1,且a1,a3,a9成等比數列,
∴a32=a1a9,即(1+2d)2=1×(1+8d), ∴4d2=8d,
∵d≠0,∴d=1. ∴an=a1+(n﹣1)=1+n﹣1=n.
(Ⅱ)∵![]() +an=2n+n,
+an=2n+n,
∴數列![]() 的前n項和Sn=
的前n項和Sn=![]() +
+![]() =2n+1﹣2+
=2n+1﹣2+![]() .
.
【方法點晴】本題主要考查等差數列的通項公式及等比數列的性質和利用“分組求和法”求數列前![]() 項和,屬于中檔題. 利用“分組求和法”求數列前
項和,屬于中檔題. 利用“分組求和法”求數列前![]() 項和常見類型有兩種:一是通項為兩個公比不相等的等比數列的和或差,可以分別用等比數列求和后再相加減;二是通項為一個等差數列和一個等比數列的和或差,可以分別用等差數列求和、等比數列求和后再相加減.
項和常見類型有兩種:一是通項為兩個公比不相等的等比數列的和或差,可以分別用等比數列求和后再相加減;二是通項為一個等差數列和一個等比數列的和或差,可以分別用等差數列求和、等比數列求和后再相加減.


 百年學典課時學練測系列答案
百年學典課時學練測系列答案 仁愛英語同步練習冊系列答案
仁愛英語同步練習冊系列答案科目:高中數學 來源: 題型:
【題目】給出以下四個命題:
①若 ![]() <
< ![]() <0,則
<0,則 ![]() +
+ ![]() >2;
>2;
②若a>b,則am2>bm2;
③在△ABC中,若sinA=sinB,則A=B;
④任意x∈R,都有ax2﹣ax+1≥0,則0<a≤4.
其中是真命題的有( )
A.①②
B.②③
C.①③
D.③④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某條公共汽車線路收支差額![]() 與乘客量
與乘客量![]() 的函數關系如圖所示(收支差額
的函數關系如圖所示(收支差額![]() 車票收入
車票收入![]() 支出費用),由于目前本條線路虧損,公司有關人員提出了兩條建議:建議(Ⅰ)不改變車票價格,減少支出費用;建議(Ⅱ)不改變支出費用,提高車票價格,下面給出的四個圖形中,實線和虛線分別表示目前和建議后的函數關系,則
支出費用),由于目前本條線路虧損,公司有關人員提出了兩條建議:建議(Ⅰ)不改變車票價格,減少支出費用;建議(Ⅱ)不改變支出費用,提高車票價格,下面給出的四個圖形中,實線和虛線分別表示目前和建議后的函數關系,則
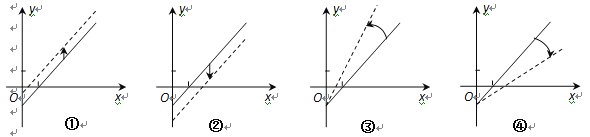
A. ①反映了建議(Ⅱ),③反映了建議(Ⅰ)
B. ①反映了建議(Ⅰ),③反映了建議(Ⅱ)
C. ②反映了建議(Ⅰ),④反映了建議(Ⅱ)
D. ④反映了建議(Ⅰ),②反映了建議(Ⅱ)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】函數 ![]() 是定義在(﹣1,1)上的奇函數,且
是定義在(﹣1,1)上的奇函數,且 ![]() .
.
(1)確定函數的解析式;
(2)證明函數f(x)在(﹣1,1)上是增函數;
(3)解不等式f(t﹣1)+f(t)<0.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知某漁船在漁港O的南偏東60°方向,距離漁港約160海里的B處出現險情,此時在漁港的正上方恰好有一架海事巡邏飛機A接到漁船的求救信號,海事巡邏飛機迅速將情況通知了在C處的漁政船并要求其迅速趕往出事地點施救.若海事巡邏飛機測得漁船B的俯角為68.20°,測得漁政船C的俯角為63.43°,且漁政船位于漁船的北偏東60°方向上.
(Ⅰ)計算漁政船C與漁港O的距離;
(Ⅱ)若漁政船以每小時25海里的速度直線行駛,能否在3小時內趕到出事地點?
(參考數據:sin68.20°≈0.93,tan68.20°≈2.50,shin63.43°≈0.90,tan63.43°≈2.00, ![]() ≈3.62,
≈3.62, ![]() ≈3.61)
≈3.61)

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知向量 ![]() =(cosα,sinα),
=(cosα,sinα), ![]() =(cosβ,sinβ),|
=(cosβ,sinβ),| ![]() ﹣
﹣ ![]() |=
|= ![]()
![]() .
.
(1)求cos(α﹣β)的值;
(2)若﹣ ![]() <β<0<α<
<β<0<α< ![]() ,且sinβ=﹣
,且sinβ=﹣ ![]() ,求sinα的值.
,求sinα的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某市統計局就某地居民的月收入調查了10 000人,并根據所得數據畫出樣本的頻率分布直方圖如圖所示.(每個分組包括左端點,不包括右端點,如第一組表示[1 000,1 500)。

(1)求居民收入在[2000,3 000)的頻率;
(2)根據頻率分布直方圖算出樣本數據的中位數;
(3)為了分析居民的收入與年齡、職業等方面的關系,必須按月收入再從這10 000人中按分層抽樣方法抽出100人作進一步分析,則月收入在[2 000,3 000)的這段應抽取多少人?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖甲所示, ![]() 是梯形
是梯形![]() 的高,
的高, ![]() ,
, ![]() ,
, ![]() ,先將梯形
,先將梯形![]() 沿
沿![]() 折起如圖乙所示的四棱錐
折起如圖乙所示的四棱錐![]() ,使得
,使得![]() ,點
,點![]() 是線段
是線段![]() 上一動點.
上一動點. 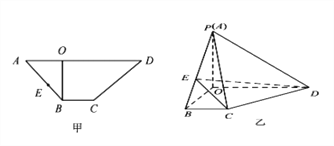
(1)證明: ![]() ;
;
(2)當![]() 時,求
時,求![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com