【題目】自點A(-3，3)發(fā)出的光線L射到x軸上，被x軸反射，其反射光線所在直線與圓x2+y2-4x-4y+7=0相切，求光線L所在直線的方程。
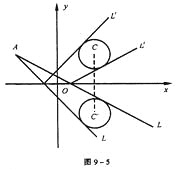
【答案】已知圓的標準方程是(x-2)2+(y-2)2=1，它關于x軸的對稱圓的方程是(x-2)2+(y+2)2=1。設光線L所在的直線的方程是y-3=k(x+3)（其中斜率k待定），由題設知對稱圓的圓心C′（2，-2）到這條直線的距離等于1，即d=
=1。整理得 12k2+25k+12=0，解得k= -
或k= -
。故所求直線方程是y-3= -(x+3)，或y-3= -(x+3)，即3x+4y-3=0或4x+3y+3=0。
【解析】試題分析：已知圓
關于
軸的對稱圓
的方程為
2分
如圖所示．
可設光線
所在直線方程為
， 4分
∵直線與圓相切，
∴圓心
到直線的距離
＝， 6分
解得
或
. 10分
∴光線所在直線的方程為
或
.…12分
科目：高中數學 來源： 題型：
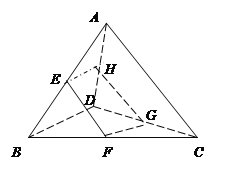
【題目】已知空間四邊形
， 
分別在
上，
(1) 若
，異面直線
與
所成的角的大小為
，求
和
所成的角的大小；
(2)當四邊形
是平面四邊形時，試判斷
與
三條直線的位置關系，并選擇其中一種位置關系說明理由；
(3)已知當
，異面直線
所成角為
，當四邊形
是平行四邊形時，試判斷
點在什么位置時，四邊形
的面積最大，試求出最大面積并說明理由。
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】△ABC的內角A，B，C所對的邊分別為a，b，c， 
=（ 
，1）， 
=（sinA，cosA）， 與 的夾角為60°． （Ⅰ）求角A的大小；
（Ⅱ）若sin（B﹣C）=2cosBsinC，求 
的值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】下列說法正確的是（ ）
A. 有一個面是多邊形，其余各面都是三角形，由這些面圍成的幾何體是棱錐
B. 有兩個面平行且相似，其余各面都是梯形的多面體是棱臺
C. 如果一個棱錐的各個側面都是等邊三角形，那么這個棱錐可能為六棱錐
D. 有兩個相鄰側面是矩形的棱柱是直棱柱
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知{an}為等差數列，且a3=﹣6，a6=0．
（1）求{an}的通項公式．
（2）若等比數列{bn}滿足b1=8，b2=a1+a2+a3 ， 求{bn}的前n項和公式．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知數列{an}的前n項和為Sn=3n﹣1．
（1）求a1 ， a2 ， a3的值；
（2）求數列{an}的通項公式；
（3）求數列{nan}的前n項和Tn ．
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
