Question

【題目】已知等差數列{an}的前n項和為Sn=n2+pn+q（p，q∈R），且a2 ， a3 ， a5成等比數列．
（1）求p，q的值；
（2）若數列{bn}滿足an+log2n=log2bn ， 求數列{bn}的前n項和Tn ．

Answer 1

【答案】
（1）

解法一：

當n=1時，a1=S1=1+p+q，

當n≥2時，an=Sn﹣Sn﹣1…（2分）

=n2+pn+q﹣[（n﹣1）2+p（n﹣1）+q]

=2n﹣1+p．

∵{an}是等差數列，

∴1+p+q=2×1﹣1+p，得q=0．

又a2=3+p，a3=5+p，a5=9+p

∵a2，a3，a5成等比數列，

∴ ，即（5+p）2=（3+p）（9+p），

解得p=﹣1．

解法二：

設等差數列{an}的公差為d，

則 ．

∵ ，

∴ ， ，q=0．

∴d=2，p=a1﹣1，q=0．

∵a2，a3，a5成等比數列，

∴ ，

即 ．

解得a1=0．

∴p=﹣1．

（2）

解法一：

由（1）得an=2n﹣2．

∵an+log2n=log2bn，

∴ ．

∴Tn=b1+b2+b3+…+bn﹣1+bn

=40+2×41+3×42+…+（n﹣1）4n﹣2+n4n﹣1，①

，②

①﹣②得 = = ．

∴

解法二：

由（1）得an=2n﹣2．

∵an+log2n=log2bn，

∴ ．

∴Tn=b1+b2+b3+…+bn﹣1+bn

=40+2×41+3×42+…+（n﹣1）4n﹣2+n4n﹣1．

由 ，

兩邊對x取導數得，

x0+2x1+3x2+…+nxn﹣1= ．

令x=4，得 ．

∴

【解析】解法一：（1）a1=S1=1+p+q，an=Sn﹣Sn﹣1=2n﹣1+p，由此求出q=0，由a2 ， a3 ， a5成等比數列，得p=﹣1．（2）an=2n﹣2， ，由此利用錯位相減法能求出數列{bn}的前n項和Tn ．
解法二：（1）由 ，得d=2，p=a1﹣1，q=0．由a2 ， a3 ， a5成等比數列，得p=﹣1．（2）an=2n﹣2. ，由 ，兩邊對x取導數得，由此能求出 ．
【考點精析】掌握數列的前n項和和等差數列的性質是解答本題的根本，需要知道數列{an}的前n項和sn與通項an的關系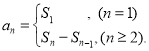；在等差數列{an}中，從第2項起，每一項是它相鄰二項的等差中項；相隔等距離的項組成的數列是等差數列．