
【題目】已知x∈R,符號[x]表示不超過x的最大整數,若函數f(x)=![]() (x>0),則給出以下四個結論:
(x>0),則給出以下四個結論:
①函數f(x)的值域為[0,1];
②函數f(x)的圖象是一條曲線;
③函數f(x)是(0,+∞)上的減函數;
④函數g(x)=f(x)﹣a有且僅有3個零點時![]() .
.
其中正確的序號為 .
【答案】④
【解析】解:由于符號[x]表示不超過x的最大整數,函數f(x)=![]() (x>0),
(x>0),
取x=﹣1.1,則[x]=﹣2,∴f(x)=![]() >1,故①不正確.
>1,故①不正確.
由于當0<x<1,[x]=0,此時f(x)=0;
當1≤x<2,[x]=1,此時f(x)=![]() ;
;
當2≤x<3,[x]=2,此時f(x)=![]() , 此時
, 此時![]() <f(x)≤1,
<f(x)≤1,
當3≤x<4,[x]=3,此時f(x)=![]() , 此時
, 此時![]() <g(x)≤1,
<g(x)≤1,
當4≤x<5,[x]=4,此時f(x)=![]() , 此時
, 此時![]() <g(x)≤1,
<g(x)≤1,
故f(x)的圖象不會是一條曲線,且 f(x)不會是(0,+∞)上的減函數,故排除②、③.
函數g(x)=f(x)﹣a有且僅有3個零點時,函數f(x)的圖象和直線y=a有且僅有3個交點,
此時,![]() , 故④正確,
, 故④正確,
所以答案是:④.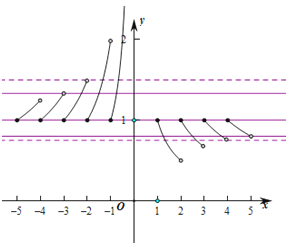


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】從某居民區隨機抽取10個家庭,獲得第i個家庭的月收入xi(單位:千元)與月儲蓄yi(單位:千元)的數據資料,算得 ![]() =80,
=80, ![]() =20,
=20, ![]() iyi=184,
iyi=184, ![]()
![]() =720.(b=
=720.(b= 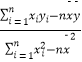 )
)
(1)求家庭的月儲蓄y對月收入x的線性回歸方程;
(2)判斷變量x與y之間是正相關還是負相關;
(3)若該居民區某家庭月收入為7千元,預測該家庭的月儲蓄.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=ax2+bx+c,滿足f(1)=﹣![]() , 且3a>2c>2b.
, 且3a>2c>2b.
(1)求證:a>0時,![]() 的取值范圍;
的取值范圍;
(2)證明函數f(x)在區間(0,2)內至少有一個零點;
(3)設x1 , x2是函數f(x)的兩個零點,求|x1﹣x2|的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】5個球放入3個盒子,在下列不同條件下,各有多少種投放方法?
①小球不同,盒子不同,盒子不空
②小球不同,盒子不同,盒子可空
③球不同,盒子相同,盒子不空
④小球不同,盒子相同,盒子可空
⑤小球相同,盒子不同,盒子不空
⑥小球相同,盒子不同,盒子可空
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列四個函數:①y=3-x;②y=![]() ;③y=x2+2x-10;④y=-
;③y=x2+2x-10;④y=-![]() .其中值域為R的函數個數有( )
.其中值域為R的函數個數有( )
A. 1個 B. 2個
C. 3個 D. 4個
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為增強市民的環保意識,某市面向全市增招環保知識義務宣傳志愿者,從符合條件的志愿者中隨機選取![]() 名志愿者,其年齡頻率分布直方圖如圖所示,其中年齡(歲)分成五組:第
名志愿者,其年齡頻率分布直方圖如圖所示,其中年齡(歲)分成五組:第![]() 組
組![]() ,第
,第![]() 組
組![]() ,第
,第![]() 組
組![]() ,第
,第![]() 組
組![]() ,第
,第![]() 組
組![]() ,得到的頻率分布直方圖(局部)如圖所示.
,得到的頻率分布直方圖(局部)如圖所示.
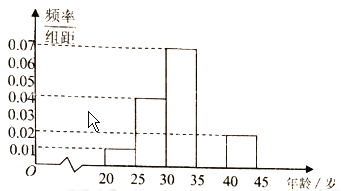
(1)求第![]() 組的頻率,并在圖中補畫直方圖;
組的頻率,并在圖中補畫直方圖;
(2)從![]() 名志愿者中再選出年齡低于
名志愿者中再選出年齡低于![]() 歲的志愿者
歲的志愿者![]() 名擔任主要宣講人,求這
名擔任主要宣講人,求這![]() 名主要宣講人的年齡在不同一組的概率.
名主要宣講人的年齡在不同一組的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】用二分法研究函數f(x)=x3+3x﹣1的零點時,第一次經計算f(0)<0,f(0.5)>0,可得其中一個零點x0∈ ,第二次應計算的f(x)的值為f( ).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某銷售公司為了解員工的月工資水平,從1000位員工中隨機抽取100位員工進行調查,得到如下的頻率分布直方圖:
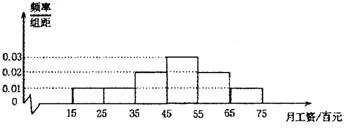
(1)試由此圖估計該公司員工的月平均工資;
(2)該公司工資發放是以員工的營銷水平為重要依據來確定的,一般認為,工資低于4500。元的員工屬于學徒階段,沒有營銷經驗,若進行營銷將會失敗;高于4500元的員工是具備營銷成熟員工,基進行營銷將會成功。現將該樣本按照“學徒階段工資”、“成熟員工工資”分成兩層,進行分層抽樣,從中抽出5人,在這5人中任選2人進行營銷活動。活動中,每位員工若營銷成功,將為公司贏得3萬元,否則公司將損失1萬元。試問在此次比賽中公司收入多少萬元的可能性最大?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,若Ω是長方體ABCD﹣A1B1C1D1被平面EFGH截去幾何體EFGHB1C1后得到的幾何體,其中E為線段A1B1上異于B1的點,F為線段BB1上異于B1的點,且EH∥A1D1 , 則下列結論中不正確的是( )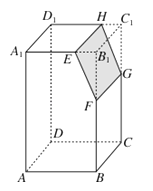
A.EH∥FG
B.四邊形EFGH是矩形
C.Ω是棱柱
D.Ω是棱臺
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com