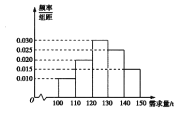
【題目】經銷商經銷某種農產品，在一個銷售季度內，每售出
該產品獲利潤500元，未售出的產品，每
虧損300元.根據歷史資料，得到銷售季度內市場需求量的頻率分布直方圖，如圖所示.經銷商為下一個銷售季度購進了
該農產品.以
(單位: 
)表示下一個銷售季度內的市場需求量， 
(單位:元）表示下一個銷售季度內經銷該農產品的利潤.
（1）將
表示為
的函數；
（2）根據直方圖估計利潤
不少于57000元的概率；
（3）在直方圖的需求量分組中，以各組的區間中點值代表該組的各個值，并以需求量落入該區間的頻率作為需求量取該區間中點值的概率(例如:若需求量
，則取
，且
的概率等于需求量落入
的頻率），求
的數學期望.
名校練考卷期末沖刺卷系列答案科目：高中數學 來源： 題型：
【題目】已知直線x﹣9y﹣8=0與曲線C：y=x3﹣px2+3x相交于A，B，且曲線C在A，B處的切線平行，則實數p的值為（ ）
A.4
B.4或﹣3
C.﹣3或﹣1
D.﹣3
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】10.已知{an}是正數組成的數列，a1=1，且點( 
，an+1)(n∈N*)在函數y=x2+1的圖象上.
（1）求數列{an}的通項公式.
（2）若數列{bn}滿足b1=1，bn+1=bn+ 
，求證：bn·bn+2< 
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
中心在坐標原點,焦點在坐標軸上,且經過
三點.
(1)求橢圓
的方程;
(2)在直線
上任取一點
,連接
,分別與橢圓
交于
兩點,判斷直線
是否過定點?若是,求出該定點.若不是,請說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】(本題共12分）已知函數
(1)討論
的單調性；
(2)是否存在常數
，使
對任意的
和任意的
都成立，若存在，求出t的取值范圍；若不存在，請說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知數列{an}中，a1=1，前n項和Sn= 
an ．
（1）求a2 ， a3 ， 及{an}的通項公式．
（2）求{ 
}的前n項和Tn ， 并證明：1≤Tn＜2．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知數列
，其前
項和為
.
（1）若對任意的
， 
， 
， 
組成公差為4的等差數列，且
，求
；
（2）若數列
是公比為
（
）的等比數列， 
為常數，
求證：數列
為等比數列的充要條件為
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
