
【題目】實驗杯足球賽采用七人制淘汰賽規則,某場比賽中一班與二班在常規時間內戰平,直接進入點球決勝環節,在點球決勝環節中,雙方首先輪流罰點球三輪,罰中更多點球的球隊獲勝;若雙方在三輪罰球中未分勝負,則需要進行一對一的點球決勝,即雙方各派處一名隊員罰點球,直至分出勝負;在前三輪罰球中,若某一時刻勝負已分,尚未出場的隊員無需出場罰球(例如一班在先罰球的情況下,一班前兩輪均命中,二班前兩輪未能命中,則一班、二班的第三位同學無需出場).由于一班同學平時踢球熱情較高,每位隊員罰點球的命中率都能達到0.8,而二班隊員的點球命中串只有0.5,比賽時通過抽簽決定一班在每一輪都先罰球.
(1)定義事件![]() 為“一班第三位同學沒能出場罰球”,求事件
為“一班第三位同學沒能出場罰球”,求事件![]() 發生的概率;
發生的概率;
(2)若兩隊在前三輪點球結束后打平,則進入一對一點球決勝,一對一球決勝由沒有在之前點球大戰中出場過的隊員主罰點球,若在一對一點球決勝的某一輪中,某對隊員射入點球且另一隊員未能射入,則比賽結束;若兩名隊員均射入或者均射失點球,則進行下一輪比賽. 若直至雙方場上每名隊員都已經出場罰球,則比賽亦結束,雙方通過抽簽決定勝負,本場比賽中若已知雙方在點球大戰,以隨機變量![]() 記錄雙方進行一對一點球決勝的輪數,求
記錄雙方進行一對一點球決勝的輪數,求![]() 的分布列與數學期望.
的分布列與數學期望.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】在△ABC中,內角A,B,C的對邊分別為a,b,c,已知2ccosA+a=2b
(1)求角C的值;
(2)若c=2,且△ABC的面積為 ![]() ,求a,b.
,求a,b.
查看答案和解析>>
科目: 來源: 題型:
【題目】2000多年前,古希臘大數學家阿波羅尼奧斯((Apollonius)發現:平面截圓錐的截口曲線是圓錐曲線.已知圓錐的高為![]() ,
, ![]() 為地面直徑,頂角為
為地面直徑,頂角為![]() ,那么不過頂點
,那么不過頂點![]() 的平面;與
的平面;與![]() 夾角
夾角![]() 時,截口曲線為橢圓;與
時,截口曲線為橢圓;與![]() 夾角
夾角![]() 時,截口曲線為拋物線;與
時,截口曲線為拋物線;與![]() 夾角
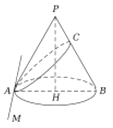
夾角![]() 時,截口曲線為雙曲線.如圖,底面內的直線
時,截口曲線為雙曲線.如圖,底面內的直線![]() ,過
,過![]() 的平面截圓錐得到的曲線為橢圓,其中與
的平面截圓錐得到的曲線為橢圓,其中與![]() 的交點為
的交點為![]() ,可知
,可知![]() 為長軸.那么當
為長軸.那么當![]() 在線段
在線段![]() 上運動時,截口曲線的短軸頂點的軌跡為( )
上運動時,截口曲線的短軸頂點的軌跡為( )
A. 圓的部分 B. 橢圓的部分 C. 雙曲線的部分 D. 拋物線的部分
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在平面直角坐標系![]() 中,以坐標原點
中,以坐標原點![]() 為極點,
為極點, ![]() 軸正半軸為極軸建立極坐標系,已知曲線
軸正半軸為極軸建立極坐標系,已知曲線![]() 的極坐標方程為:
的極坐標方程為: ![]() ,直線
,直線![]() 的參數方程是
的參數方程是![]() (
(![]() 為參數,
為參數, ![]() ).
).
(1)求曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)設直線![]() 與曲線
與曲線![]() 交于兩點
交于兩點![]() ,且線段
,且線段![]() 的中點為
的中點為![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在銳角△ABC中,內角A,B,C的對邊分別為a,b,c,且2asinB= ![]() b.
b.
(1)求角A的大小;
(2)若a=6,b+c=8,求△ABC的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=x2﹣kx+(2k﹣3).
(1)若k= ![]() 時,解不等式f(x)>0;
時,解不等式f(x)>0;
(2)若f(x)>0對任意x∈R恒成立,求實數k的取值范圍;
(3)若函數f(x)兩個不同的零點均大于 ![]() ,求實數k的取值范圍.
,求實數k的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設△ABC的內角A,B,C的對邊分別為a,b,c,已知4sinA=4cosBsinC+bsin2C,且C≠ ![]() .
.
(1)求c;
(2)若C= ![]() ,求△ABC周長的取值范圍.
,求△ABC周長的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=|x﹣3|﹣|x﹣a|.
(1)當a=2時,解不等式f(x)≤﹣ ![]() ;
;
(2)若存在實數x,使得不等式f(x)≥a成立,求實數a的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com