
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 是菱形,且
是菱形,且![]() .點
.點
![]() 是棱
是棱![]() 的中點,平面
的中點,平面![]() 與棱
與棱![]() 交于點
交于點![]() .
.

(1)求證:![]() ∥
∥![]() ;
;
(2)若![]() ,且平面
,且平面![]() 平面
平面![]() ,求平面
,求平面![]() 與平面
與平面![]() 所成的銳二面角的余弦值.
所成的銳二面角的余弦值.
【答案】(1)證明見解析;(2)![]() .
.
【解析】
試題分析:對于(1),先根據菱形的性質得到![]() ,進而得到
,進而得到![]() 面
面![]() ,接下來根據
,接下來根據![]() 四點共面,且平面
四點共面,且平面![]() 平面
平面![]() ,即可得到結論;對于(2),取
,即可得到結論;對于(2),取![]() 中點
中點![]() ,連接
,連接![]() ,根據等腰三角形的性質以及線面垂直的知識得到
,根據等腰三角形的性質以及線面垂直的知識得到![]() ,進而根據菱形的性質得到
,進而根據菱形的性質得到![]() ,建立空間直角坐標系
,建立空間直角坐標系![]() ,利用向量運算解決.
,利用向量運算解決.
試題解析:(1)證明:因為底面![]() 是菱形,所以
是菱形,所以![]() .
.
又因為![]() 面
面![]() ,
,![]() 面
面![]() ,所以
,所以![]() 面
面![]() .
.
又因為![]() 四點共面,且平面
四點共面,且平面![]() 平面
平面![]() ,
,
所以![]() .
.
(2)取![]() 中點
中點![]() ,連接
,連接![]() .因為
.因為![]() ,所以
,所以![]() .又因為平面
.又因為平面![]() 平面
平面![]() ,且平面
,且平面![]() 平面
平面![]() , 所以
, 所以![]() 平面
平面![]() .所以
.所以![]() .在菱形
.在菱形![]() 中,因為
中,因為![]() 是
是![]() 中點,所以
中點,所以![]() .
.
如圖,建立空間直角坐標系![]() .設
.設![]() ,
,
則![]() .
.
又因為![]() ,點
,點![]() 是棱
是棱![]() 中點,所以點
中點,所以點![]() 是棱
是棱![]() 中點.所以
中點.所以![]() .所以
.所以![]() .
.
設平面![]() 的法向量為
的法向量為![]() ,則有
,則有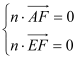 所以
所以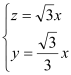
令![]() ,則平面
,則平面![]() 的一個法向量為
的一個法向量為![]() .
.
因為![]() 平面
平面![]() ,所以
,所以![]() 是平面
是平面![]() 的一個法向量.
的一個法向量.
因為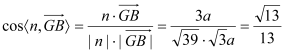 ,
,
所以平面![]() 與平面
與平面![]() 所成的銳二面角的余弦值為
所成的銳二面角的余弦值為![]() .
.



科目:高中數學 來源: 題型:
【題目】已知有窮數列:![]() ,
,![]() ,
,![]() ,……,
,……,![]()
![]() 的各項均為正數,且滿足條件:
的各項均為正數,且滿足條件:
①![]() ;②
;②![]() .
.
(1)若![]() ,
,![]() ,求出這個數列;
,求出這個數列;
(2)若![]() ,求
,求![]() 的所有取值的集合;
的所有取值的集合;
(3)若![]() 是偶數,求
是偶數,求![]() 的最大值(用
的最大值(用![]() 表示).
表示).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某投資公司計劃投資A,B兩種金融產品,根據市場調查與預測,A產品的利潤y1與投資金額x的函數關系為y1=18-![]() ,B產品的利潤y2與投資金額x的函數關系為y2=
,B產品的利潤y2與投資金額x的函數關系為y2=![]() (注:利潤與投資金額單位:萬元).
(注:利潤與投資金額單位:萬元).
(1)該公司已有100萬元資金,并全部投入A,B兩種產品中,其中x萬元資金投入A產品,試把A,B兩種產品利潤總和表示為x的函數,并寫出定義域;
(2)在(1)的條件下,試問:怎樣分配這100萬元資金,才能使公司獲得最大利潤?其最大利潤為多少萬元?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設數列![]() 的前
的前![]() 項和為
項和為![]() ,
, ![]() 且
且![]() 成等差數列。
成等差數列。
(1證明![]() 為等比數列,并求數列
為等比數列,并求數列![]() 的通項;
的通項;
(2)設![]() ,且
,且![]() ,證明
,證明![]() 。
。
(3)在(2)小問的條件下,若對任意的![]() ,不等式
,不等式![]() 恒成立,試求實數λ的取值范圍.
恒成立,試求實數λ的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,已知圓
中,已知圓![]() 過坐標原點
過坐標原點![]() 且圓心在曲線
且圓心在曲線![]() 上.
上.
(1)若圓![]() 分別與
分別與![]() 軸、
軸、![]() 軸交于點
軸交于點![]() 、
、![]() (不同于原點
(不同于原點![]() ),求證:
),求證:![]() 的面積為定值;
的面積為定值;
(2)設直線![]() 與圓
與圓![]() 交于不同的兩點
交于不同的兩點![]() ,且
,且![]() ,求圓
,求圓![]() 的方程;
的方程;
(3)設直線![]() 與(2)中所求圓
與(2)中所求圓![]() 交于點
交于點![]() 、
、![]() ,
, ![]() 為直線
為直線![]() 上的動點,直線
上的動點,直線![]() ,
,![]() 與圓
與圓![]() 的另一個交點分別為
的另一個交點分別為![]() ,
,![]() ,且
,且![]() ,
,![]() 在直線
在直線![]() 異側,求證:直線
異側,求證:直線![]() 過定點,并求出定點坐標.
過定點,并求出定點坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某高中有高一新生500名,分成水平相同的![]() 兩類教學實驗,為對比教學效果,現用分層抽樣的方法從
兩類教學實驗,為對比教學效果,現用分層抽樣的方法從![]() 兩類學生中分別抽取了40人,60人進行測試
兩類學生中分別抽取了40人,60人進行測試
(1)求該學校高一新生![]() 兩類學生各多少人?
兩類學生各多少人?
(2)經過測試,得到以下三個數據圖表:
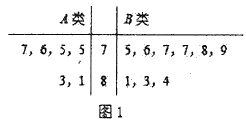
圖1:75分以上![]() 兩類參加測試學生成績的莖葉圖
兩類參加測試學生成績的莖葉圖
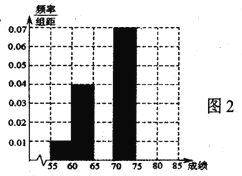
圖2:100名測試學生成績的頻率分布直方圖
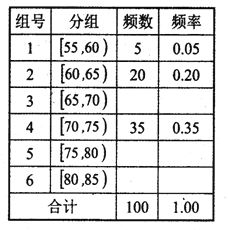
下圖表格:100名學生成績分布表:
①先填寫頻率分布表中的六個空格,然后將頻率分布直方圖(圖2)補充完整;
②該學校擬定從參加考試的79分以上(含79分)的![]() 類學生中隨機抽取2人代表學校參加市比賽,求抽到的2人分數都在80分以上的概率.
類學生中隨機抽取2人代表學校參加市比賽,求抽到的2人分數都在80分以上的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《九章算術》是我國古代數學成就的杰出代表,其中《方田》章有弧田面積計算問題,計算術曰:以弦乘矢,矢又自乘,并之,二而一.其大意是,弧田面積計算公
式為:弧田面積=![]() ,弧田是由圓弧(簡稱為弧田弧)和以圓
,弧田是由圓弧(簡稱為弧田弧)和以圓
弧的兩端為頂點的線段(簡稱為弧田弦)圍成的平面圖形,公式中“弦”指的是弧
田弦的長,“矢”等于弧田弧所在圓的半徑與圓心到弧田弦的距離之差.現有一弧
田,其弦長AB等于6米,其弧所在圓為圓O,若用上述弧田面積計算公式算得該
弧田的面積為![]() 平方米,則cos∠AOB= ( )
平方米,則cos∠AOB= ( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com