
【題目】某商品在近30天內每件的銷售價格P元和時間t(t∈N)的關系如圖所示.
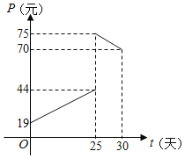
(1)請確定銷售價格P(元)和時間t(天)的函數解析式;
(2)該商品的日銷售量Q(件)與時間t(天)的關系是:Q=﹣t+40(0≤t≤30,t∈N),求該商品的日銷售金額y(元)與時間t(天)的函數解析式;
(3)求該商品的日銷售金額y(元)的最大值,并指出日銷售金額最大的一天是30天中的哪一天?
【答案】(1)![]() ;(2)
;(2)![]() ;
;
(3)第25天,日銷售金額有最大值1125元.
【解析】
(1)根據已知中的圖象可得函數是一個分段函數,分0≤t<25和25≤t≤30,t∈N兩種情況,利用待定系數法可分別求出兩段的解析式,最后綜合討論結果可得答案;(2)根據商品的日銷售量Q(件)與時間t(天)的關系是:Q=﹣t+40(0≤t≤30,t∈N),結合(1)中銷售價格P(元)和時間t(天)的函數解析式,根據:日銷售金額=銷售價格×銷售量得到答案;(3)根據(2)中函數的解析式,結合二次函數的圖象和性質,求出函數的最大值點及最大值,可得答案.
(1)當0≤t<25,t∈N,設P=at+b,將(0,19),(25,44)代入得![]() ,解之得
,解之得![]() ,∴P=t+19(0≤t<25,t∈N),當25≤t≤30,t∈N,同理可得P=﹣t+100,
,∴P=t+19(0≤t<25,t∈N),當25≤t≤30,t∈N,同理可得P=﹣t+100,
綜上所述:銷售價格P(元)和時間t(天)的函數解析式為![]() .
.
(2)由題意得,y=PQ,由(1)得![]() ,
,
即:![]() .
.
(3)由![]() ,
,
當0≤t<25,t∈N,由二次函數的圖象和性質知t=10,或t=11時,y取最大值870元
當25≤t≤30,t∈N,由二次函數的圖象和性質知t=25時,y取最大值1125元
綜上所述,在第25天,日銷售金額有最大值1125元


 同步練習強化拓展系列答案
同步練習強化拓展系列答案科目:高中數學 來源: 題型:
【題目】中國古代數學名著《九章算術》中有這樣一個問題:今有牛、馬、羊食人苗,苗主責之粟五斗,羊主曰:“我羊食半馬.”馬主曰:“我馬食半牛.”今欲衰償之,問各出幾何?此問題的譯文是:今有牛、馬、羊吃了別人的禾苗,禾苗主人要求賠償5斗粟.羊主人說:“我羊所吃的禾苗只有馬的一半.”馬主人說:“我馬所吃的禾苗只有牛的一半.”打算按此比例償還,他們各應償還多少?已知牛、馬、羊的主人各應償還![]() 升,
升, ![]() 升,
升, ![]() 升,1斗為10升,則下列判斷正確的是( )
升,1斗為10升,則下列判斷正確的是( )
A. ![]() ,
, ![]() ,
, ![]() 依次成公比為2的等比數列,且
依次成公比為2的等比數列,且![]()
B. ![]() ,
, ![]() ,
, ![]() 依次成公比為2的等比數列,且
依次成公比為2的等比數列,且![]()
C. ![]() ,
, ![]() ,
, ![]() 依次成公比為
依次成公比為![]() 的等比數列,且
的等比數列,且![]()
D. ![]() ,
, ![]() ,
, ![]() 依次成公比為
依次成公比為![]() 的等比數列,且
的等比數列,且![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設拋物線y2=8x的焦點為F,過點F作直線l與拋物線分別交于A,B兩點,若點M滿足 ![]() =
= ![]() (
( ![]() +
+ ![]() ),過M作y軸的垂線與拋物線交于點P,若|PF|=4,則M點的橫坐標為 .
),過M作y軸的垂線與拋物線交于點P,若|PF|=4,則M點的橫坐標為 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一裝有水的直三棱柱ABC-A1B1C1容器(厚度忽略不計),上下底面均為邊長為5的正三角形,側棱為10,側面AA1B1B水平放置,如圖所示,點D、E、F、G分別在棱CA、CB、C1B1、C1A1上,水面恰好過點D,E,F,C,且CD=2

(1)證明:DE∥AB;
(Ⅱ)若底面ABC水平放置時,求水面的高
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,已知AB為圓O的直徑,C,D是圓O上的兩個點,CE⊥AB于E,BD交AC于G,交CE于F,CF=FG. 
(1)求證:AC是∠DAB的平分線;
(2)求證:OF∥AG.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知a>0且滿足不等式22a+1>25a﹣2.
(1)求實數a的取值范圍;
(2)求不等式loga(3x+1)<loga(7﹣5x);
(3)若函數y=loga(2x﹣1)在區間[1,3]有最小值為﹣2,求實數a的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】拋物線![]() (
(![]() )的焦點為
)的焦點為![]() ,已知點
,已知點![]() ,
, ![]() 為拋物線上的兩個動點,且滿足
為拋物線上的兩個動點,且滿足![]() .過弦
.過弦![]() 的中點
的中點![]() 作拋物線準線的垂線
作拋物線準線的垂線![]() ,垂足為
,垂足為![]() ,則
,則![]() 的最大值為__________.
的最大值為__________.
【答案】1
【解析】設![]() ,在三角形ABF中,用余弦定理得到
,在三角形ABF中,用余弦定理得到![]()
![]() ,
, 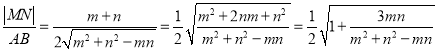
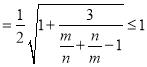 故最大值為1.
故最大值為1.
故答案為:1.
點睛:本題主要考查了拋物線的簡單性質.解題的關鍵是利用了拋物線的定義。一般和拋物線有關的小題,很多時可以應用結論來處理的;平時練習時應多注意拋物線的結論的總結和應用。尤其和焦半徑聯系的題目,一般都和定義有關,實現點點距和點線距的轉化。
【題型】填空題
【結束】
17
【題目】設![]() 的內角
的內角![]() ,
, ![]() ,
, ![]() 所對的邊分別為
所對的邊分別為![]() ,
, ![]() ,
, ![]() ,且
,且![]() ,
, ![]() .
.
(1)當![]() 時,求
時,求![]() 的值;
的值;
(2)當![]() 的面積為
的面積為![]() 時,求
時,求![]() 的周長.
的周長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com